模型压缩
Why edge device 低延迟,高隐私
分类两条路线:
- 软件加速
- 硬件加速
Software
Network pruning
模型剪枝
模型具备很多参数(神经元),并不一定所有参数都有作用,找到没有用处的参数并作修剪,成为模型剪枝
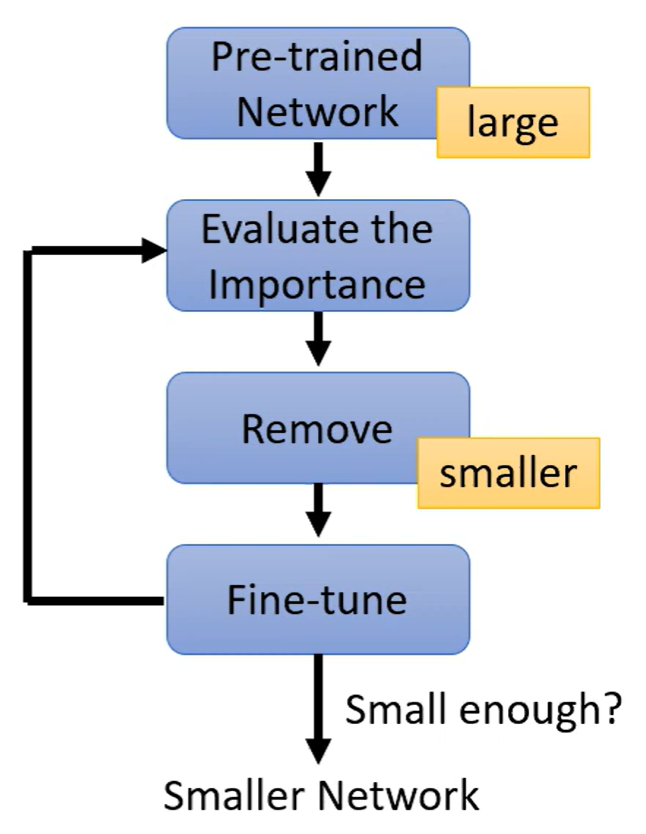
训练模型—测量参数(神经元)的重要性—移除不重要的参数—微调来恢复性能—再次修剪—直到模型符合预期
需要注意的是,如果是以参数作为单位进行修剪的话,产生的网络是不规则的,不利于实现和GPU加速
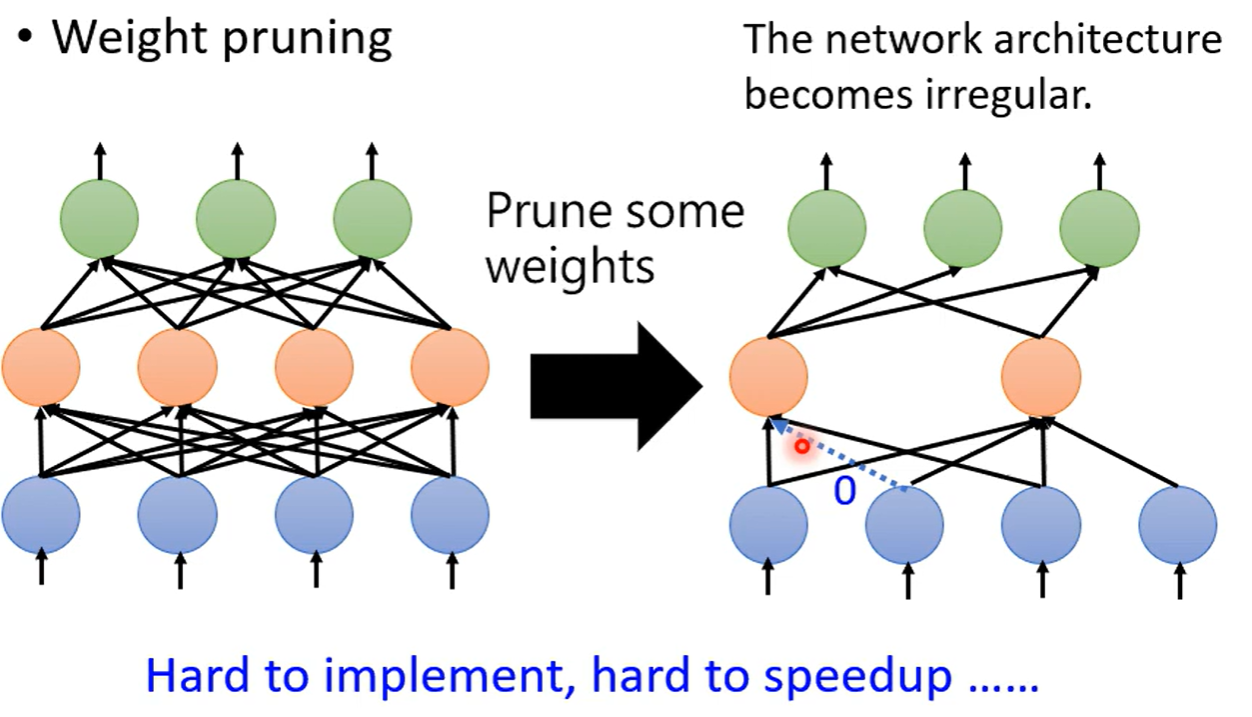
一般就算参数为0也会记录下参数,否则无法进行矩阵运算,但是这样一来参数的修剪效果就大打折扣
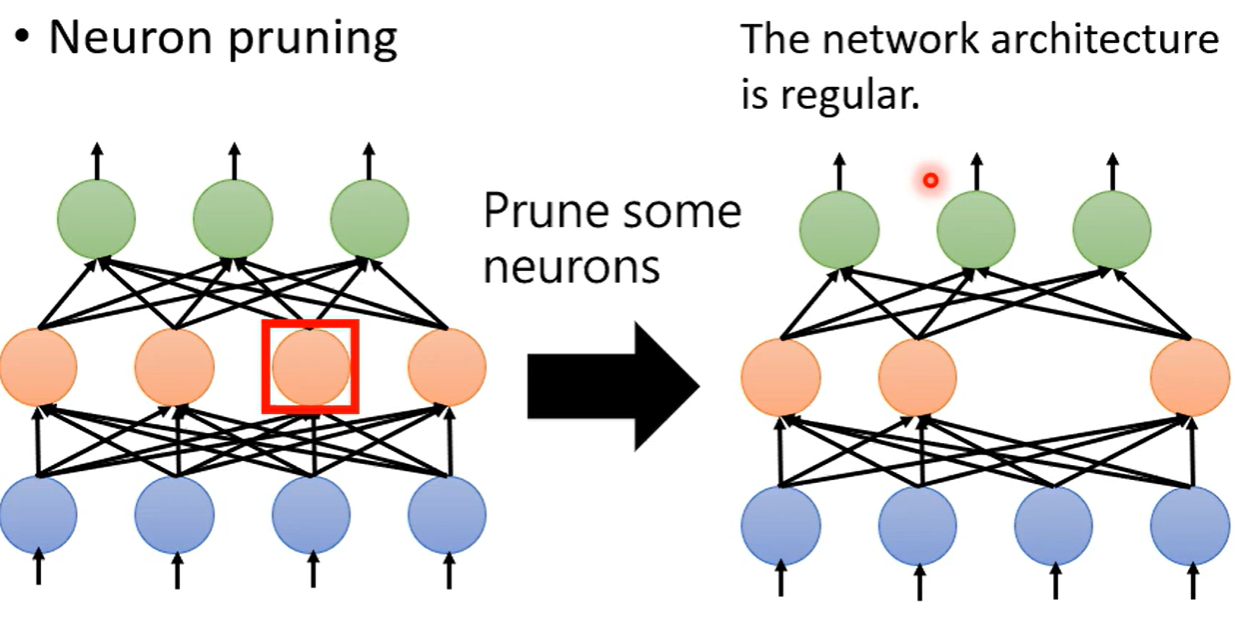
而用神经元修剪,则形状规则,可以作矩阵加速
why not smaller
为什么不训练一个小的模型?
- 大模型比较好训练
- 大模型精度高
Lottery Ticket Hypothesis 大乐透假说,可以认为大模型中包含多个小模型,只要有一些小模型训练成功了,大模型就成功,与彩票购买逻辑相似。 实验:尝试将大模型剪枝否的小模型结构重新训练,发现随机参数train不了,只有与大模型参数相同才可以成功
sign-ificance 后来在实验中证明并不一定要求参数完全一致,只要符号一致,数值不重要
Knowledge Distillation
Teacher模型的输出直接给Student 学习,Teacher模型可以不止一个,多个模型ensemble也可以
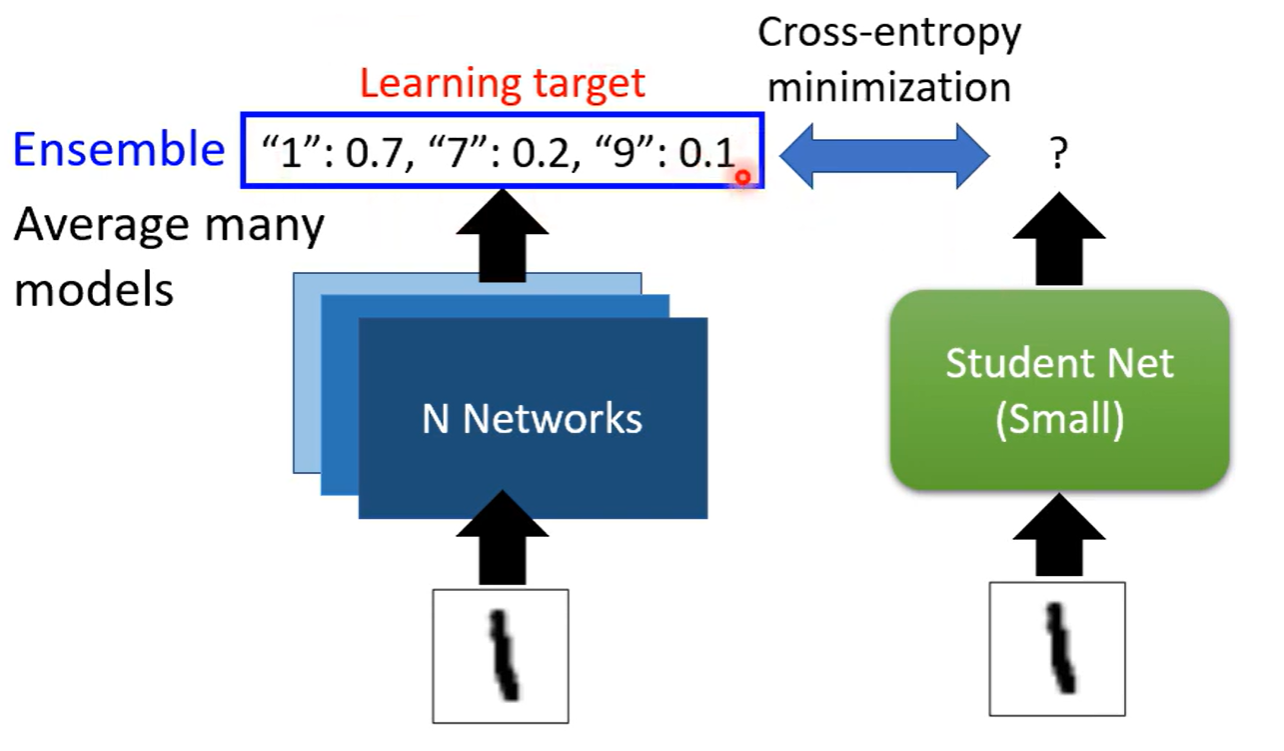
Temperature 给softmax的结果增加一个温度参数,目的是平滑输出,但是结果不变,将平滑的输出给student学习,结果才会好

Parameter Quantization
参数量化
- Less bits to represent a value
- Weight clustering
- Huffman encoding
压缩参数,减少存储空间,有时精度甚至会比较好
Architecture Design
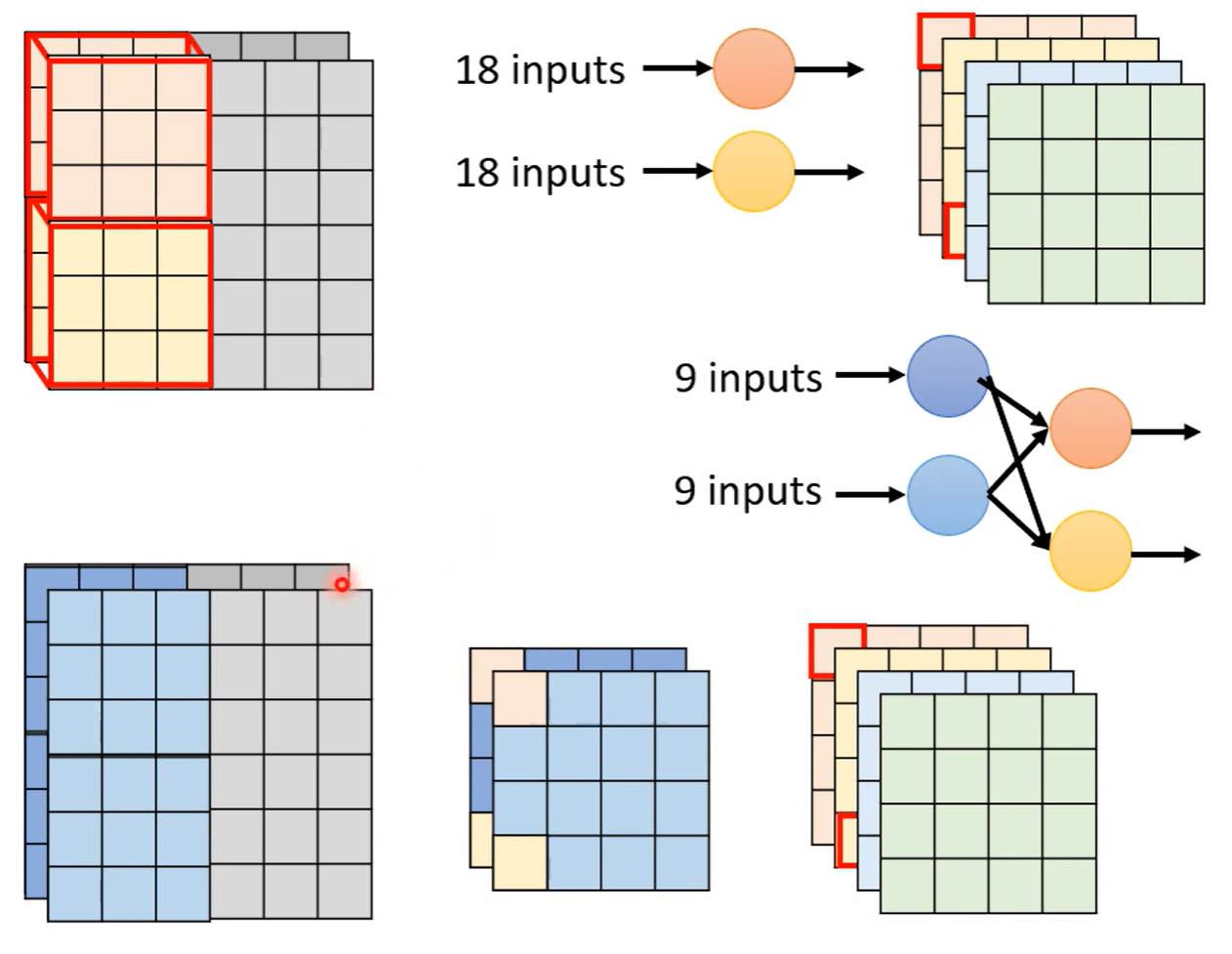
Depthwise Separable Convolution
一般情况下的卷积Filter是自定义数量的,在Depthwise 卷积下,FIlter的数量随通道数决定,每一个通道使用一个卷积核
但是这样收集不到通道之间的资讯,所以再设计Pointwise Convolution,用1 * 1 * c 的卷积对Depthwise卷积的结果做卷积

O是通道数,k是卷积核大小,通道数很大,可以忽略不计,也就是参数减少为之前的
How
Low rank approximation 通过增加一层来减少参数量,两层网络(假设全连接)之间的参数量由层神经元数量之积决定,即M * N,如果增加一层数量比较少的K,参数量就是 N * K + K * M,如果K足够小,那么参数量就会减少
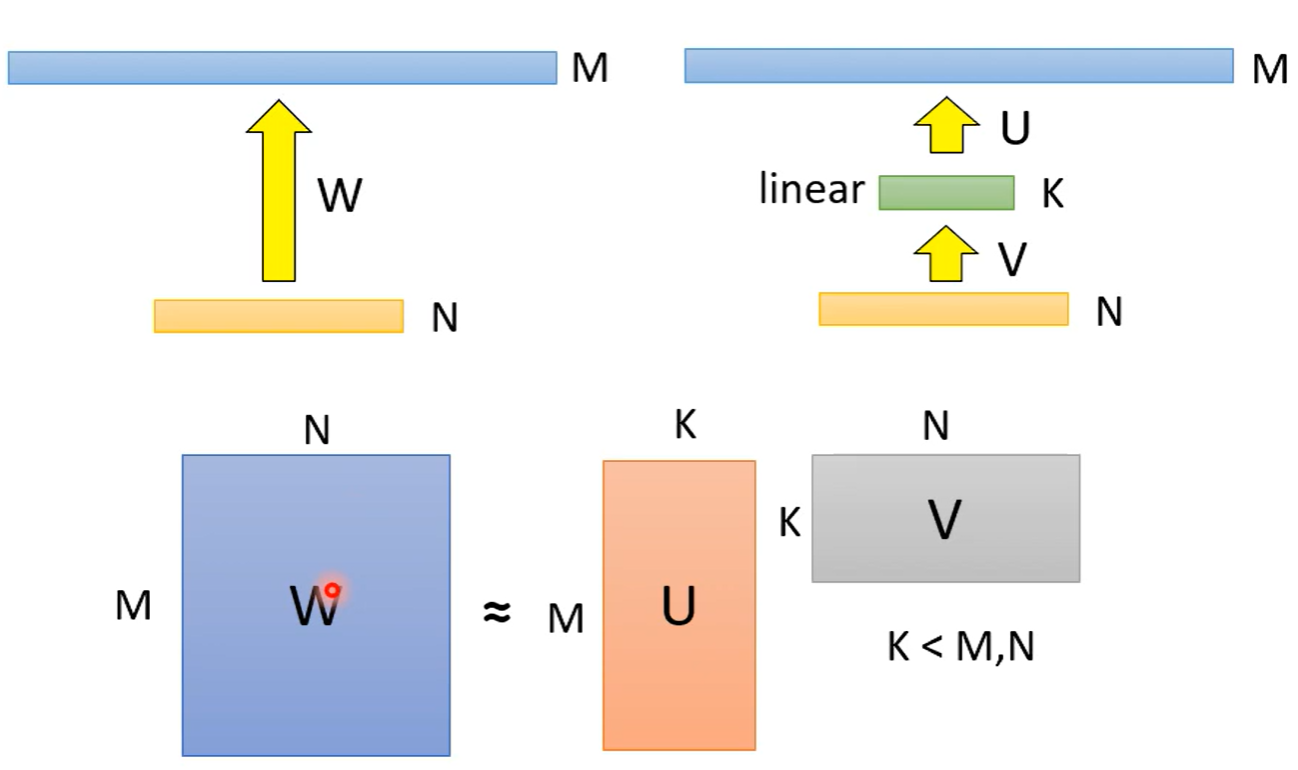
但是参数的rank会减少,小于等于K,实际上对参数做了一些限制
实际上Depthwise卷积就是区分通道数,将原来一个卷积核得到的姐结果分成两个结果,再通过Pointwise合并成一个,与原来相比多了一层
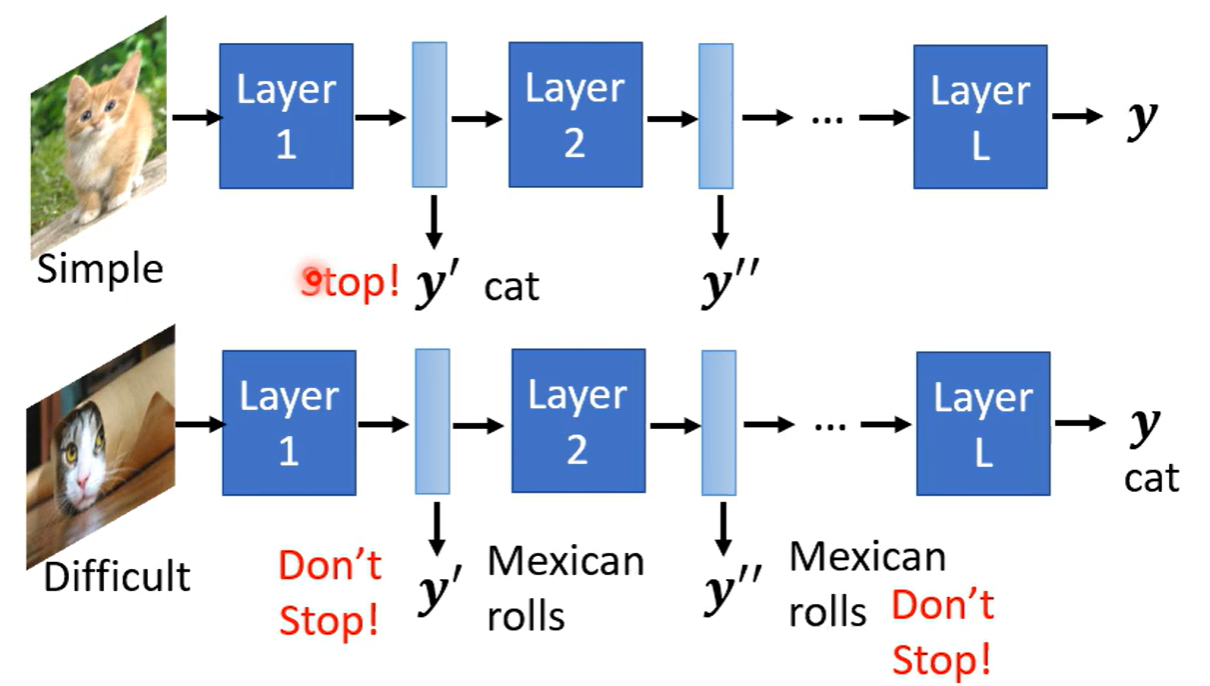
Dynamic Computation
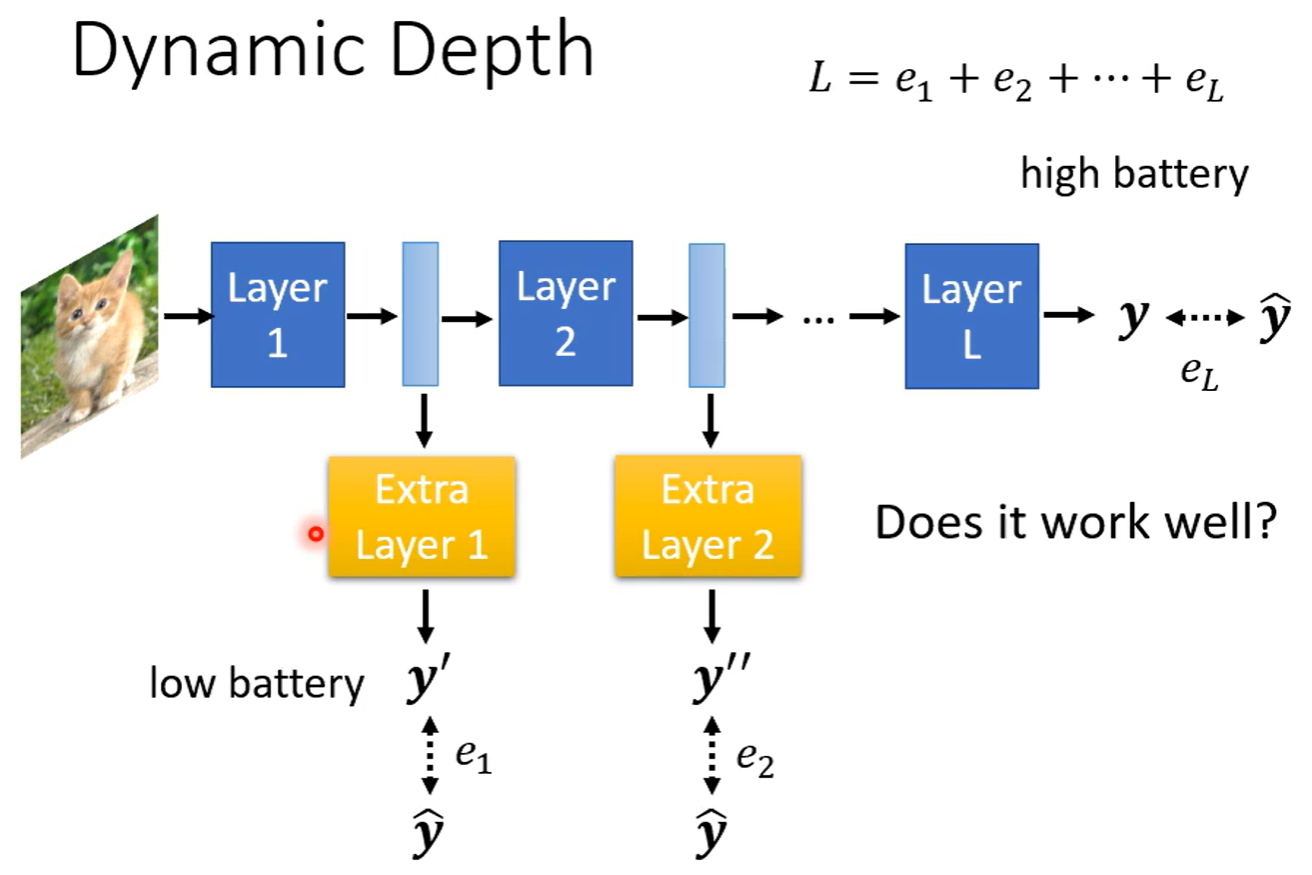
动态计算
模型动态调整运算量
例如以深度划分,不同层次输出代表不同的算力,在每一层的后面接上一层额外的输出层,计算与最ground truth的距离,加和后输出作为最终结果
宽度 动态选择神经元数量,将输出的结果与ground truth的距离,最小化距离训练不同宽度的情况
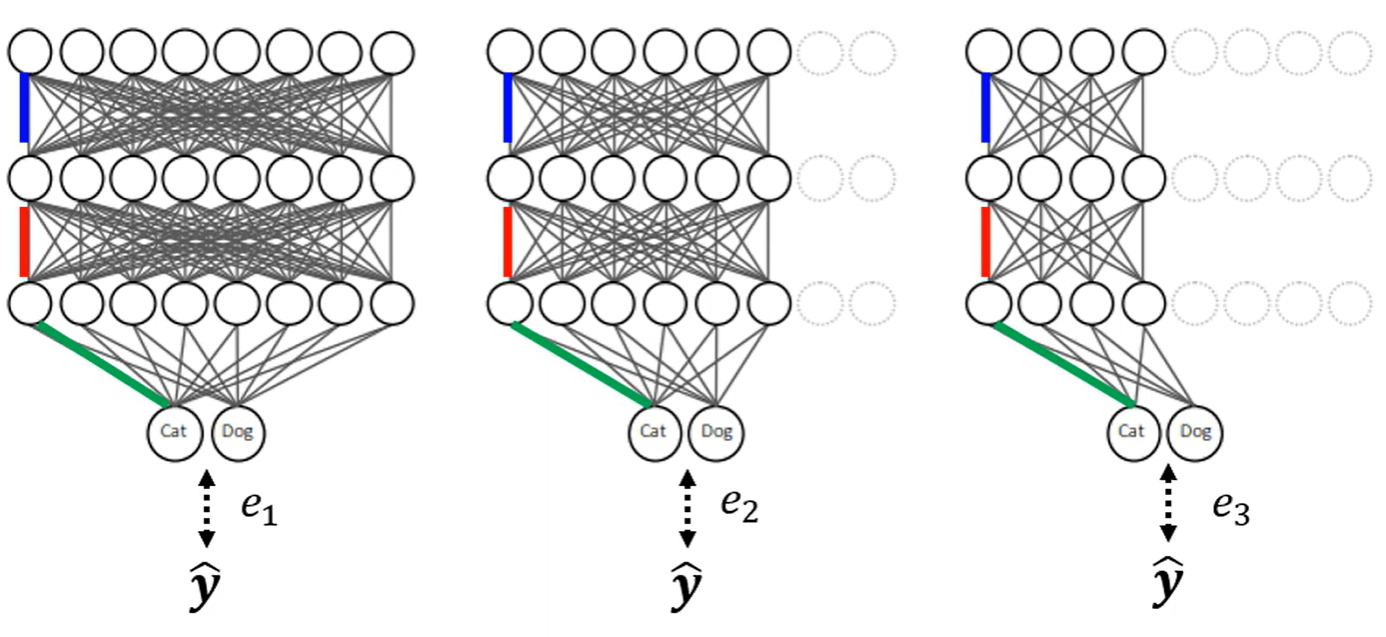
自动决定 根据任务的难易程度自动选择需要的深度,不只局限在算力不足,在不同任务下也可以节省算力