ML 入门 W1

机器学习相关的知识其实吴恩达的视频已经比较详尽，在此记录下总结性与新的点

概论

机器学习两大任务：

• 回归
• 分类

实际上AI的难题： Structured Learning

创造一个有结构的物品，例如图像，文档

名词定义

MAE mean absolute error

MSE mean square erroe(MSE)

Error surface 不同参数下损失函数的视图

hyperparameters 超参数 所有需要自己调节的参数

Local minima 局部最优（小）

global minima 全局最优（小）

新的知识

Local minima不是深度学习梯度下降法的主要问题

模型的限制称为 model bias 这种限制可以是由于特征量太少，或者是模型太简单，梯度下降到极致也得不到理想的损失

层次多的模型认为其弹性大

data augmentation 图像反转，镜像等从的原有数据进行数据增加

i. i. d

independently and identically distributed 独立同分布，大多数情况下要求数据集满足独立同分布，一般可以假设满足

1-of-N encoding

一种特征的表示方式，用 01 来表明特征是否存在，存在为1，否则为0

beyond 1-of-N encoding

1-of-N encoding的表示方法中需要实现确定不同特征对应的向量的位置，如果遇到实现没确定过的特征就无法表示，可以增加一个other特征，如果有这样的特征，就加到other

多锯齿与Sigmoid

锯齿线段组成的曲线称为 Piecewise Linear 其可以由多个小的锯齿线段组合而成

一个多锯齿的曲线可以逼近任何的连续曲线

而一个小的锯齿曲线可以用Sigmoid曲线来拟合

所以这个小锯齿曲线可以称为hard Sigmoid

所以逻辑是，调整很多的b，w值来构造很多的Sigmoid函数来拟合Hard Sigmoid曲线来组成所需的预测曲线

多个Sigmoid可以组合成更复杂的曲线

用ReLU也可以，因为ReLU的形状大概是sigmoid的一半，两个ReLU可以组成一个sigmoid，实现一样的功能

Optimization issue

优化算法不能找到优解的问题 可以通过小一点的模型，或者机器学习算法试做，如果其loss可以降低，但是深度学习模型的loss却不可以，那么就是Optimization问题

一般层次大的可以做到层次小的，因为深层可以什么都不做来做到层次浅的模型的效果，如果深层的模型反而做不到低的loss，则很可能是找不到优解

N-fold Cross Balidation

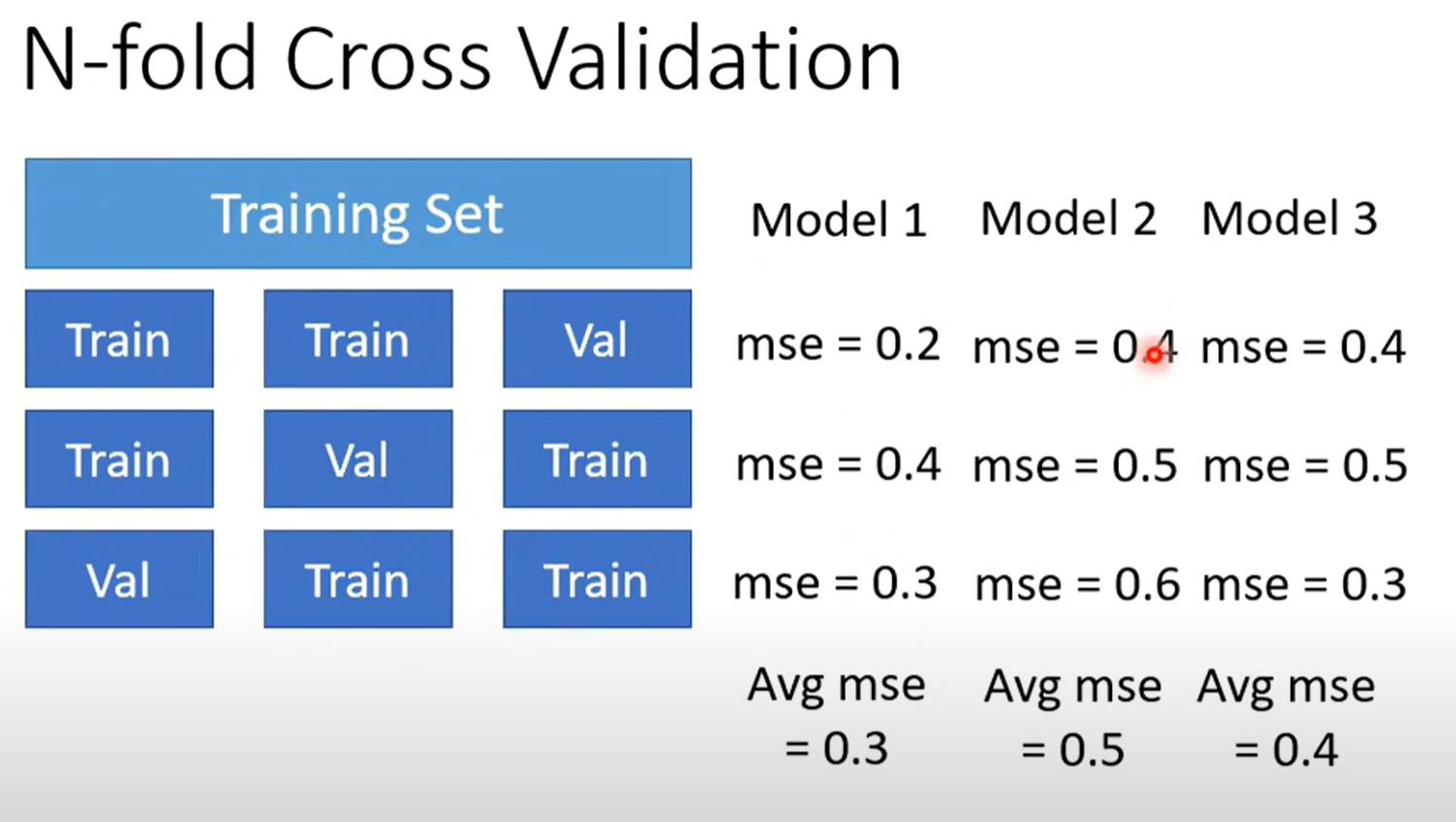划分例如三等分，两份为训练，一份做验证

分别做训练与验证，将不同的模型的结果取平均，值最小的模型认为精度最高

训练

局部最小与鞍点

局部最小(local minima)是损失函数降不下最常见的原因之一，但不是所有可能性都是局部最小，可能因为损失函数进入到鞍点(Saddle Point)

鞍点是几个维度的低点，同时是其他维度的高点，梯度为0，与局部最小一致

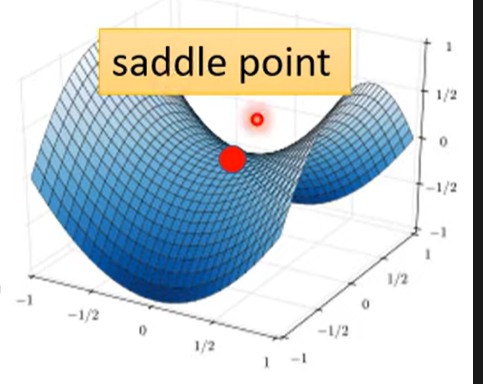
梯度为0的点称为critical point

如何判断当前是鞍点还是局部最小点？

构造函数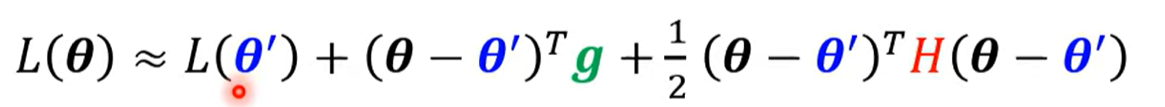： g是梯度，H是hessian矩阵

这个函数为泰勒级数近似(Tayler Series Approximation)

含义是取一个距离相近的点，用这个点的值来进似，后面的项是数学方法使得近似结果更准确

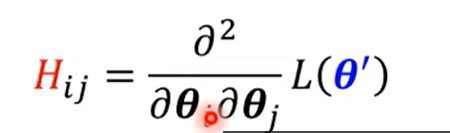
当走到critical point，梯度为0，只剩下Hessian矩阵，通过矩阵可以判断函数的error surface，来判断是局部最小还是鞍点

如果取 ${\theta }^{\prime }$ 怎么取，$L(\theta )都大于L({\theta }^{\prime })$ ，说明这个点是局部最小，反之局部最大

如果有大有小，就是鞍点

一般通过Hessian矩阵的特征值来判断，如果特征值都是正的，那么局部最小，都是负的，那么局部最大，有正有负，那么鞍点

如果判断出来是鞍点的话，可以跳出鞍点，找到更优解

首先损失函数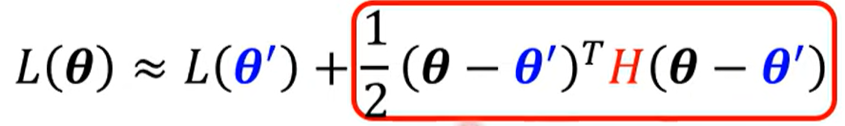

由矩阵特征值 (eigen value) 的定义可以求得下式

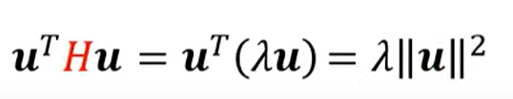
• 如果\lambda是负的，那么上式结果就是负的
• 如果上式就是损失函数的红色块的值，那么损失函数就可以变小

\lambda 小于0一定存在（鞍点定义） 通过将$\theta -{\theta }^{\prime }=u->\theta ={\theta }^{\prime }+u$ 就可以跳出鞍点

但是实际上求解Hessian矩阵很复杂，所以实际不用，而是用其他方法代替

假说

三体中有一段从石棺中取物，从三维空间找不到路，到了四维空间就可以找到

Deep Learning的训练也存在类似的假说，在二维空间的局部最小会不会就是三维空间的鞍点？是否可以同理推广呢？是否越高的维度实际上局部最小点就越少呢？

参数的数量决定了维度，多少参数就有多少维度，实验可以看到确实是局部最小点很少出现

Batch 和 Momentum

批次与动量

批次就是每次训练的最小数据量，每个批次单独计算损失，但是参数是同步优化的

每个epoch分一次Batch，每次Batch都不一样

Batch

Batch size 大小对计算有一定的影响 size决定训练的更新

• size小，每次更新快（不考虑平行计算），但是优化效果不稳定，因此参照的数据少，优化不一定对
• size大，更新慢，优化较稳定 但是在平行计算之下，Batch内容可以并行计算，不一定花费时间受size影响大，

虽然size的大小会影响一次更新的时间，其其越大时间越长，Batch size的大小会影响到batch的数量，batch的数量越大，实际上一个epoch花的时间就越短。

但是另外，size越小，训练时实际存在噪音，但是训练之后的精确度却会更高（或许是精细训练的结果）

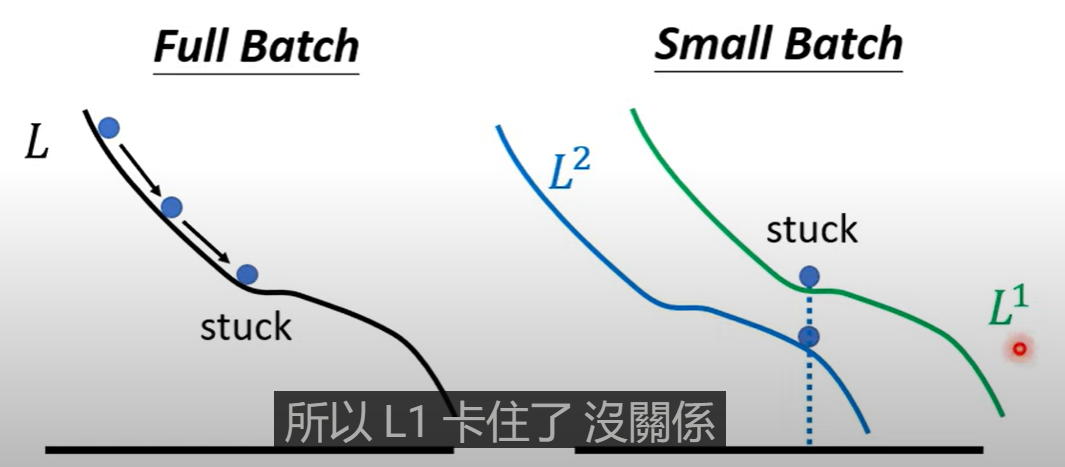
一种可能是：每次训练用的是这一次的batch来更新参数，这个损失卡在critical point了，一样的参数值不一定在损失函数是critical point

同等的训练精度下，小的Batch对测试集的精度比大的更高

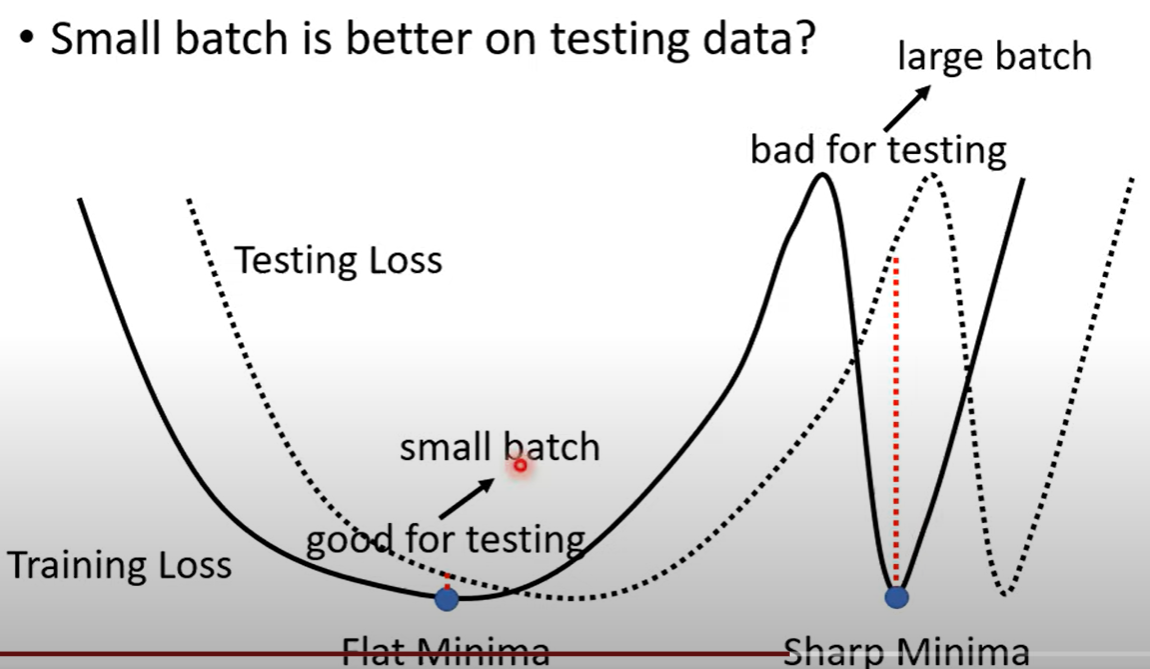
当训练找到的优解在较平缓的最低值与陡峭的最低值，在测试时的精度可能存在差异，假设测试集的损失函数在训练集的损失函数基础上平移一点，那么在陡峭的最低值变化会剧烈过在平缓的最低值，使得测试集的精度低于训练集，小的Batch可能倾向于达到平缓的最低值

Momentum

球在下坡时会存在一定动量（冲力），到达局部最优的时候会再冲一小段距离，这让跳出局部最优成为可能

动量的概念在于：梯度下降时，每次不止考虑当前梯度的反方向，还考虑前一次变化的方向，两者加权求得这一次前进的方向。

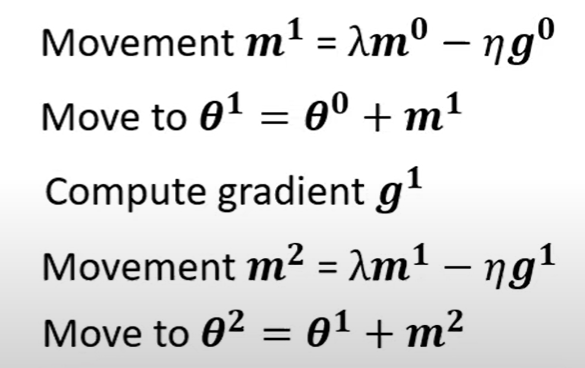
代入m可以发现m其实与所有梯度的加权之和 也就是动量实际上也可以认为是在进行梯度下降时，同时考虑前面所有梯度

Training stuck

上述讨论了局部最小和鞍点等导致梯度下降失效的问题，但实际上损失函数不变的原因不一定是因为卡在critical point ，即梯度不一定就变得很小，而是可能在两个坡度之间来回变动

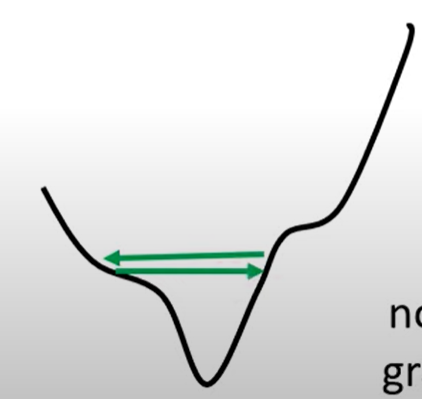
事实上使用梯度下降法卡在critical point的可能性小于梯度降不下（步长太长或太短）的可能性

自适应学习率

在原本的学习率上增加一个参数，定义为

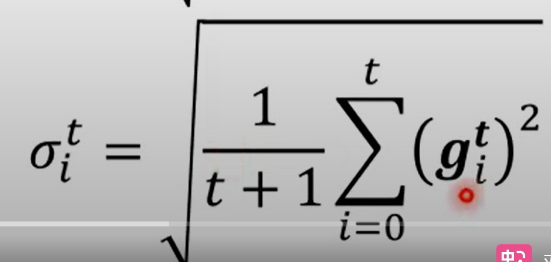
当前为止所有的梯度的平方和平均开根号

学习率定义为：

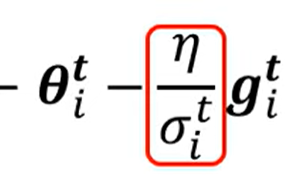
这样的定义下可以实现学习率对梯度的自适应调整，当梯度都偏大时，说明坡度陡峭，参数值会变大，学习率也就变小，步长变小，反之一致

且不同的优化参数有不同的自适应参数

这称为：APagrade

这种学习率的条这个策略存在一定缺陷，当平陡变化的时候并不能快速调整学习率

提出RMSProp

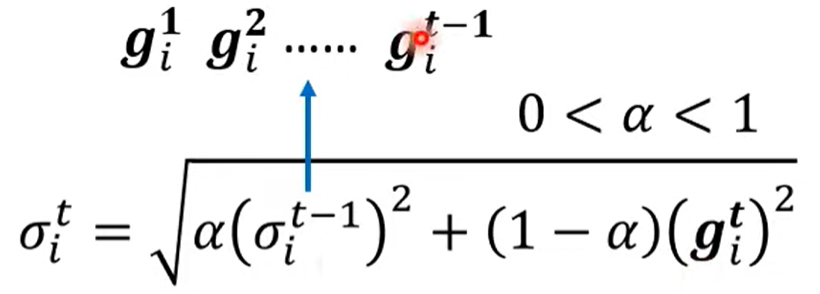
定义$\alpha$ 来选择当前梯度有前一个梯度的占比，也就是选择其对梯度变化的影响

Adam RMSProp + Momentum的结合就是当今最常用的优化器Adam

学习率调度

指随时间调整基本的学习率

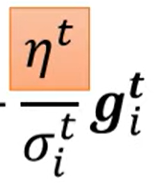
解决在后期梯度变化依旧很大的问题

一般是让学习率随时间变小，称为Learning rate decay

还有学习率先变大在变小，称为Warm up （有一种说法是先让模型在周边探索，再大胆前进，再随时间变小，数学上可以认为是因为学习率参数是一个统计值，需要数据来支撑其准确性，所以一开始步长较小来获取数据）

最终的学习率

动量，自适应参数，学习率调度等共存

分类

用回归来做分类（例如计算出来的值接近1就是类别1，接近2就是类别2）其实隐含了相邻类别之间存在相近的关系，例如1和2回归的预测值是相近的，但是两个类别却不一定有关系

此时可以用向量来表示，例如一维的为1则为第一类，2维为1则第二类等，这样类别之间就没有数值关系

计算结果通过softmax得到分类（详见 SoftMax)

损失函数 Cross-entropy 最小化这个函数就是最大化似然值

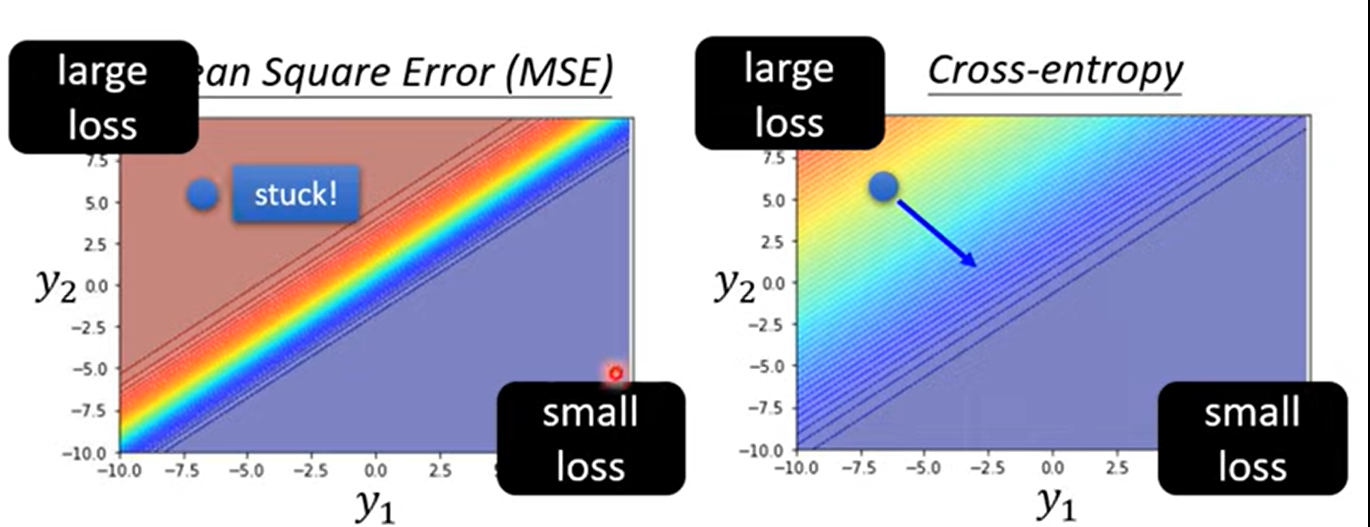
分类模型损失函数选择MSE和Cross-entropy的区别： 对数使得损失函数的斜率更明显，再如上所示的例子中，从同一起点开始训练，MSE的训练更难走出起始点（斜率不明显）

Batch Normalization

从另一个角度理解标准化

图erroe surface表明： $w_2$的变化对Loss影响大，$w_1$影响却很小

这样在训练上存在一定的问题，例如移动到最低点时，对参数$w_1$的调整很慢

Feature Normalization

数据的同一特征减去均值再除以标准差，这样一来特征的均值为0，方差为1

每一层的输入都要做标准化

不可能全部数据都一起做标准化，实际上在使用的时候只对Batch做标准化

同时又标准化可能对特征造成一定的限制，可以增加参数来让模型自己进行调整

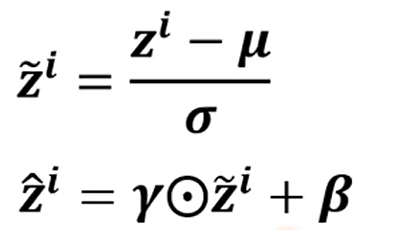
一般初始设置为1向量和0向量，之后让模型在合适的时间自己调整这两个参数

哪在testing等不确定batch的时候怎么做标准化呢？ 实际上编程时会计算moving average of $\mu$ and $\sigma$，当testing的时候，会将这个值作为标准化的参数

Pokemon and Digimon 分类器

分类基础

先观察分类依据： 发现宝可梦的线条较数码宝贝简单——通过边缘检测(edge detection)将线条提取

提取后计算线条像素点

实际上不可能取得客观存在的全部数据，我们只能得到全部数据的一小部分样本

不同的数据样本得到的学习参数是不同的，我们希望训练得到一系列参数，其对样本和数据的预测值差值相距很小，小于eps——那就等于得到一个数据，其满足对任意的参数，这个样本和全部数据的计算差值都是小于$\frac{eps}{2}$

简单推导

模型分析

分界线（学习参数）的选择不同，数据的好坏程度不同，即数据样本能否代表全部数据的概率就不同

这个概率与分界线选择的数量有关，也就是预测函数的选择数量，不同的样本数据得到不同的分界线(参数)

Hoeffding’s Inequality 霍夫丁不等式

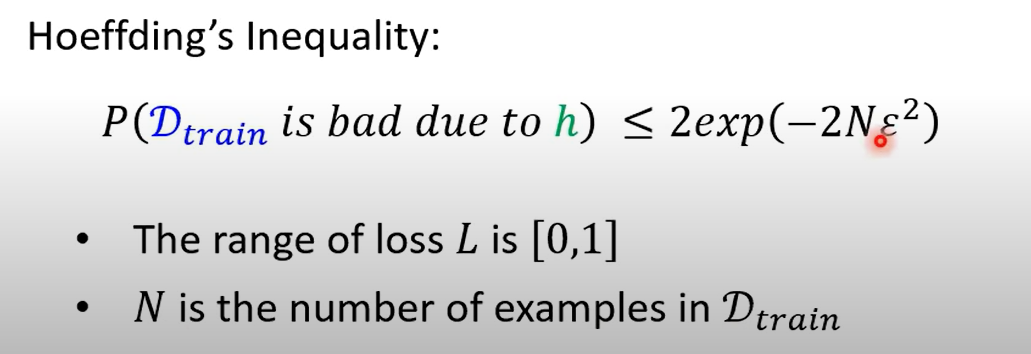
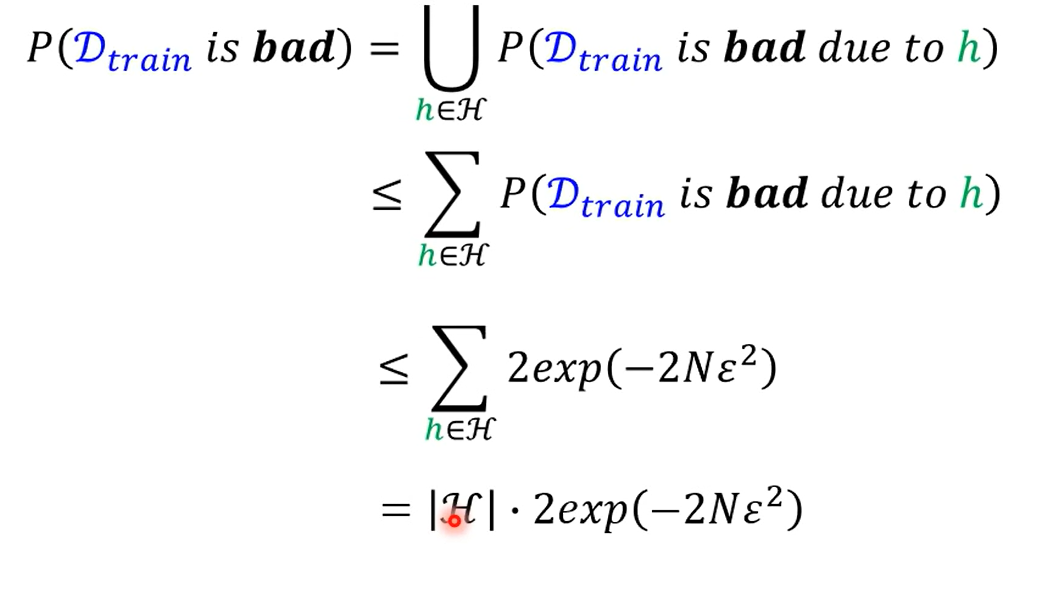
那么参数（预测函数）使得数据变差的概率就如上所示

得到结论 如果要是数据与现实数据相近 那就要满足：选择的参数的种类数量（指完整一系列参数的不同数值）减少，或原本的数据总量更大（增加训练资料）

当然参数的种类数量减少到太少，其实是理想崩坏了，能选到的参数太少

当参数的种类数量小，实际上样本数据与全部数据的损失差距小（因为有问题的数据少），反之则大 但是种类少，则一般情况下全局最好的参数在全部数据中计算出来的误差大（因为参数选择很有限）

两者矛盾，要如何解决？ 深度学习