Advanced Learning Algorithms W2

TensorFlow implementation

import tensoflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
 
model = Sequential([
		Dense(units = 25, actibation = 'sigmoid'), Dense(units = 15, activation = 'sigmoid'), Dense(units = 1, activation = 'sigmoid'),
					])
from tensorflow.keras.losser import BinaryCrossentropy
	model.compile(loss = BinaryCrossentropy())
 
	model.fit(X, Y, epochs = 100)
 
 
# BinaryCrossentropy  二元 交叉熵损失函数

1. 指定模型
2. 编译模型
3. 训练模型

模型实现

• 指定输入，输入与输出之间的计算公式 — 指定模型
• 指定损失和成本 — 编译模型 指定损失函数，编译则会让模型在之后的训练中计算该损失函数的平均值
• 最小化成本函数 — 训练模型 fit函数实现反向传播 ，即计算偏导数并实现梯度下降减少成本函数

激活函数

ReLU

Rectified Linear Unit

$g(z)=max(0,z)$

Advanced Learning Algorithms W2 2024-03-13 07.17.13.excalidraw

⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

Text Elements

Link to original

特点是，小于0就取0，大于0为线性分布，是最常使用的激活函数之一

各层与激活函数

输出层激活函数适用情形：

• sigmoid 二元分类
• linear 有正有负
• ReLU 只有非负数

隐藏层激活函数：

• ReLU 最常见 计算快，只有一边是稳定的，对梯度下降更适用，速度更快 -TensorFlow一般适用ReLU作为激活函数
• Linear 几乎没用 事实上线性回归的激活函数也是线性的，无法在逐次激活中有更复杂的内涵。如果最后一个是其他函数的话，也会直接表现为其他函数的特征。如此看来线性激活函数可以认为是没有使用激活函数
• sigmoid 常用之一 因为双边稳定，梯度下降没有ReLU那么快，在一些特殊情况适用

多类分类问题 multiclass

SoftMax 激活函数

是sigmoid的泛化拓展

假定 $z_1=w_1\cdot x_1+b_1{z}_2=w_2\cdot x_2+b_2\dots \dots z_n=w_n\cdot x_n+b_n$ 那么有 $a_i=e^{z_i}/(e^{z_1}+e^{z_2}\dots \dots +e^{z_n})=P(y=i|x)$ 表示输入为 x （矩阵）时，输出为第 i 类的概率

损失函数 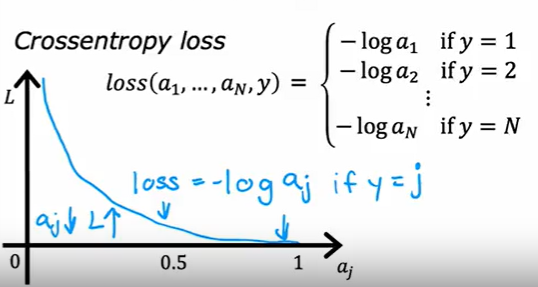同样是 sigmoid 的泛化 在TensorFlow称为 SparseCategoricalCross-entropy 函数 稀疏分类交叉熵损失函数

loss = SparseCategoricalCrossentropy()

注意到这个SoftMax是n个神经元相关的输出，这与目前接触到的函数不同（只是一个神经元的输出），这意味着有n个x的权重，n种x的选择被用来计算其中一种分类的概率

成本函数 $1\{y==n\}==\{\begin{array}{ll}1,& \text{if y==n}.\\ 0,& \text{otherwise}.\end{array}$ Now the cost is:

$$\begin{array}{r}J(\mathbf{w},b)=-\left[\sum _{i=1}^m\sum _{j=1}^{N}1\left\{y^{(i)}==j\right\}\log \frac{e^{z_j^{(i)}}}{{\sum }_{k=1}^N{e}^{z_k^{(i)}}}\right]\end{array}$$

遍历所有最终输出，每个输出遍历其类别，确认类别后计算损失函数，最后相加

更好的实现

对于像sigmoid和SoftMax的计算，由于涉及到大的分母，计算时会有浮点数参与运算，如果处理不当，由于浮点数离散的存储方式会导致在运算时精度下降。

减少中间量

在每层计算时会发现总有输出 a 作为下一层计算的中间量，如果a是sigmoid或Soft Max的输出，那么a就是浮点数运算的结果

把 a 运算过程直接在 loss 函数里进行可以减少一些误差（因为这样TensorFlow会变化计算方式来减少精度误差）

model.compile(loss = BinaryCrossEntropy(from_logits = True)) #logits 其实是z，就是把a的运算融入到loss的计算

改为这种计算后，其实输出层计算的就是线性激活函数，直接将z传到loss里

# 然后需要把概率输出
logit = model(x)
f_x = tf.nn.softmax(logits)

SoftMax 另外

SoftMax因为是指数运算，在计算时会因为指数过大等原因产生overflow错误

• 可以上下同乘一个数来减小计算结果，并且可以保证结果不变（因为是除法）

a_j = \frac{e^{z_j-C}}{ \sum_{i=1}^{N}{e^{z_i-C} }} \quad\quad\text{where}\quad C=max_j(\mathbf{z})

策略为除去最大的e指数 # 多标签分类问题 _Multi-label Classification_ 不同于数字检测等多类分类问题，多标签是对于一个输入得到多个输出，例如物体识别，图像分割 ## 实现方法 - 处理成多个机器学习 多组输入多组输出 - 将一个神经网络处理成多个输出 作为向量输出，或许每个元素对应一个标签 # 优化算法 _Advanced Optimization_ ## Adam Algorithm Adaptive Moment estimation 可以自动的调整学习率，加快成本函数的降低 ## 实现 Adam算法对每个参数有一个学习率，如果某个参数一直在往一个方向变化，就增加其学习率来加快进程；如果其梯度来回变化，就减少其学习率 ```Python model.compile(optimize = tf.keras.optimizers.Adam(learning_rate = 1e-3), los=tf.keras.losses.SparseCategoricalCrossentropy(from_logits = true) ``` # More Layer ## 卷积层 _Convolutional Layer_ 相比Dense，CNN有以下特点： - 并不读取全部特征，而是一个神经元读取一个区域的像素 - 计算更快 - 训练数据更少 - 过拟合的可能性更低 # 后向传播 _back prop_ ## 额外的数学概念 梯度究竟是什么 对于一个表达式求导的结果代表了一个数的变化趋势 如果其变量变化，函数将以导数倍的变化趋势变化，说明梯度越大变化越快 例如：$J(x) = x^2$ $x$增加$0.001$ ,那么 $J$增加 $x^2 * 0.001$ ![[Pasted image 20240316083054.png]]但是实际上并不是完全的增加 $x^2 * 0.001$，因为加上的数不是无限小，所以产生了一定的误差（理解上可以认为梯度是持续变化的，加上0.001后的梯度与不加之前的梯度不一样，用原先的数估计梯度是不准确的，如果导数是常数则不会有影响） ## 链式法则 实际上向后传播是成本函数对每一层的输出求导，一直到对输入层的输入求导。可以看成是**链式法则** ，一层一层的求导 ![[Pasted image 20240317083544.png]] 为什么用链式法则？ 其实是高效的选择，由于不同的输出构成相同的输出，从输出一层层往回算的值可以应用于不同输入的求导，而实际上算完后就只剩下代值结果应用于后面的计算，这样可以减少冗余的计算，加快传播速度 时间复杂度是$O(n + m)$ ，如果每个都重新求则是$O(nm)$ >计算图 >像上述图片的计算流程图称为计算图 Computer Graph 神经网络一般需要构建计算图来明确前向传播和后向传播