Advanced Learning Algorithms W3

评价模型

对于少数变量的模型可以通过画 特征-输出 图来与训练的数据做对比，可以得到是否过拟合，是否准确等信息

但是当特征值数量上升，画图解决不了，采用划分训练集的方法

训练集、测试集

一般通过 70% 、80%来划分训练集和测试集，训练集参与成本(cost) 函数计算，进行梯度下降， 测试集用于计算误差 测试集没有正则化计算，而是将成本函数作为误差大小的计算公式来衡量精度

测试通常为两部分

• 测试测试集 衡量测试结果是否准确，是否过拟合
• 测试训练集 衡量训练结果是否准确

只依赖于其中任一难以得到结论，相互对比可以得到更多信息

可以通过预测来计算 J_test ，而不是用逻辑损失，即预测结果 与 数据集做对比，计算不相等或大于某个误差的数据数量，以此评估模型性能

模型选择

假设要选择一个多项式模型来拟合训练集，并用测试集来评价该维度的训练结果，对多项式的维度进行遍历挑选，找到了一个最准确的维度

这实际上存在问题，改变维度来训练，再做J_test 实际上引入了参数 d，对于划分好的训练集和测试集，修改参数d来达到最好的训练结果实际上会得到 过于乐观的泛化误差

交叉验证集 cross validation set

为了解决上述问题，应用了交叉验证集(validation/development/dev set) 将数据集再划分出一个大小与测试集相近的数据集，利用这个数据集进行模型的挑选，这样避免了挑选参数d来拟合测试集，使得测试集可以计算出真实的泛化误差

泛化误差 即训练集与测试集之间的误差，用来衡量一个模型对数据的泛化程度，等于 偏差+ 方差和+数据噪声 偏差衡量拟合数据的程度，方差衡量模型对数据的稳定程度，二者往往冲突

衡量偏差与方差 Bias and variance

一般的，使用$J_{train}$来衡量拟合程度，也就是偏差

用$J_{cv}$来衡量稳定性——方差

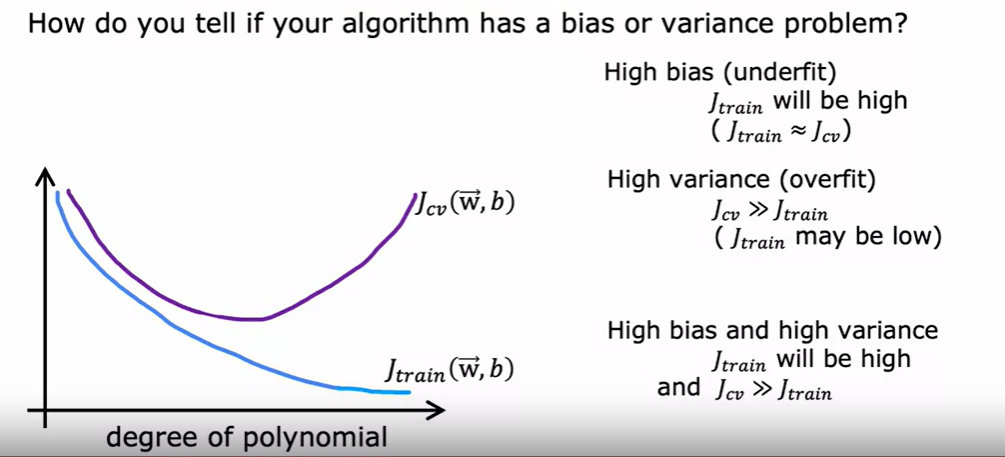
高偏差与高方差可以同时存在，当过拟合，且由于某些原因在之后的数据集上失去拟合

好的模型需要达到低偏差与方差

正则化与误差

$\lambda$的选择一定程度上可以平衡偏差与方差，使算法表现更好

当$\lambda$很大时，其作用明显，会让参数趋于0，使得训练曲线几乎不变

当$\lambda$ 很小时，对参数的控制能力小，过拟合程度加大

那要如何选择合适的$\lambda$来实现训练良好的训练效果？ 遍历$\lambda$，通过$J_{train}$和$J_{cv}$来判断得到最佳的$\lambda$值

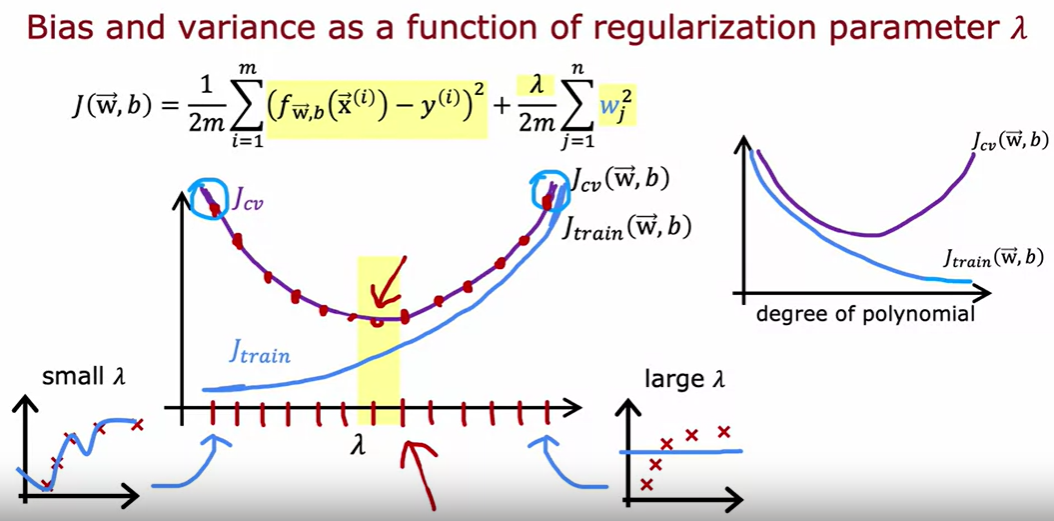$\lambda$越大，其对参数作用越强，训练结果更趋于减小参数而不是减小梯度

基线水平

基线是衡量表现好坏的标准

衡量J_train的误差是否可以接受，并不单单看数值大小，应当设立例如人类对训练集的误差来作为基线，评判性能

常见的基线选择

• 人类表现
• 竞争算法对比
• 根据经验衡量

而对于J_{cv} ，其对比的标准是与J_{train}差距大小，合理的，高性能的模型对于训练集与验证集的结果应当相近，所有一旦有偏差，且不小则可以认为具有方差的问题。

学习曲线

学习曲线具有模型训练的经验数据，很好的表现了一个模型的能力变化

对于一般的模型

如果以训练集的尺寸大小作为横坐标，两种误差作为纵坐标，会得到上述曲线

• 训练误差越来越大 因为训练数据越来越多，更难完全的拟合，因为误差越来越大

如果是高偏差的模型

当例如拟合的多项式阶数过小时，随着数据增加，拟合曲线并不随其做过多的变化，在拟合了一些数据后就趋于平缓，称为高原(plateau)。

当高偏差时，训练数据对训练结果并没有明显成效，不管数据量有多少

如果时高方差

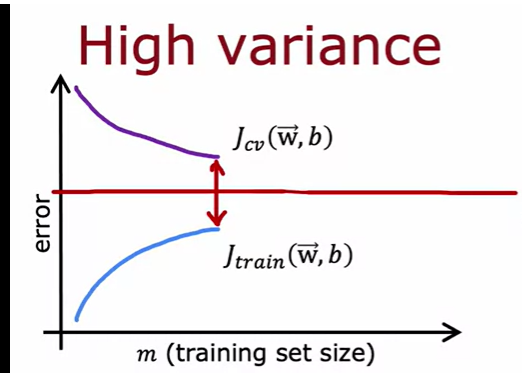当拟合程度过高，例如多项式阶数过高，会出现训练误差甚至低于基线的情况。在这种情况下增加训练数据，说不定能得到低方差的模型，因为设想一个多阶多项式在密集的数据里上下变化，当数据足够密集，则变化幅度小，方差小

实际应用

学习曲线的成本实际上很高，因为要划分不同大小的训练集做训练，一般在实际上指导意义更大，通过曲线来分析当前模型可能处于什么阶段。

• 更多训练数据 对偏差无用，对方差和可能有用
• 更少的特征 阶数高时可能拟合程度高，但方差大，更少的特征利于减少防方差
• 更多的特征 利于减少偏差
• 多项式 与特征值一样的效果
• 增加\labmda 减少，则更关注拟合，解决偏差
• 减少\labmda 增加，关注参数影响，解决方差

偏差/方差与神经网络规模

有这么一个配方式的网络训练方式：

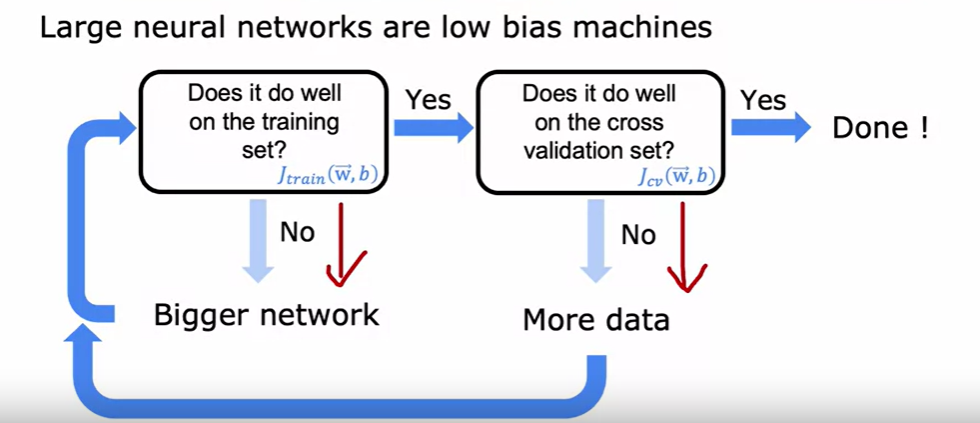
1. 如果训练误差大，就增加网络规模
2. 如果验证误差大，就说明方差问题，给更多的数据
3. 如果再发现训练误差大，再增大网络规模
4. 循环反复得到低偏差与低方差的模型

一般的，更大的网络规模往往带来更好的结果，如果发现高偏差，大的网络规模可以更好的调整参数大小来适应训练集。

但是需要合适的正则化，来避免高方差问题

缺点：

• 训练开销大，大的规模与数据毫无疑问带来更大的开销，也说明这种方式不是永无止境的

错误分析 error analysis

ML开发的迭代循环

1. 选择模型结构
2. 训练模型
3. 分析，诊断模型

如何诊断模型

取样错误的预测数据，分析共性，分类出错的各种可能 例如：

• 算法不够好
• 某一类型的数据不够多
• 特征不够全 分析哪些对进一步提升性能有大的帮助，从而决定下一步

训练集方法

数据增加

• 特定数据的增加 找特定的训练数据，或为已有的但未有标签的训练数据分类写上标签，作为新训练数据

• 数据增强 (data-centric) 图像类和音频类

  图像：旋转，缩放，对比度，镜像，扭曲(distortions) 来实现更多的更泛化的数据

  音频：背景音增加或变化，再录音

  文字：通过与现实图片相近的图片来合成数据，比如现实的手写笔记，用计算机的不同字体来增加数据

  而数据增强一般不考虑噪音，因为测试集中一般不存在噪音的数据

迁移学习(Transfer learning)

预训练模型的迁移

将以训练好的模型用于新的预测目标(任务可以几乎不同，但要求同类数据，同个网络)

改变预测目标意味着改变输出结果，至少有一层的参数值，参数量需要修改

但是其他参数却不一定要修改，可以认为：模型在训练时前面的隐藏层实现了数据基本特征的提取与计算，而且这样的特征比较泛化（例如图像类识别曲线，拐角，线条），可以用于不同的数据

利用已用的预训练权重，再训练一个符合目标的模型，可以减少训练时间，提高训练效率

步骤为：

• 监督预训练(surpervised pretraining)
• 调参(fine tuning)

完整的训练实例

界定目标 - 收集数据 - 模型训练 - 部署模型

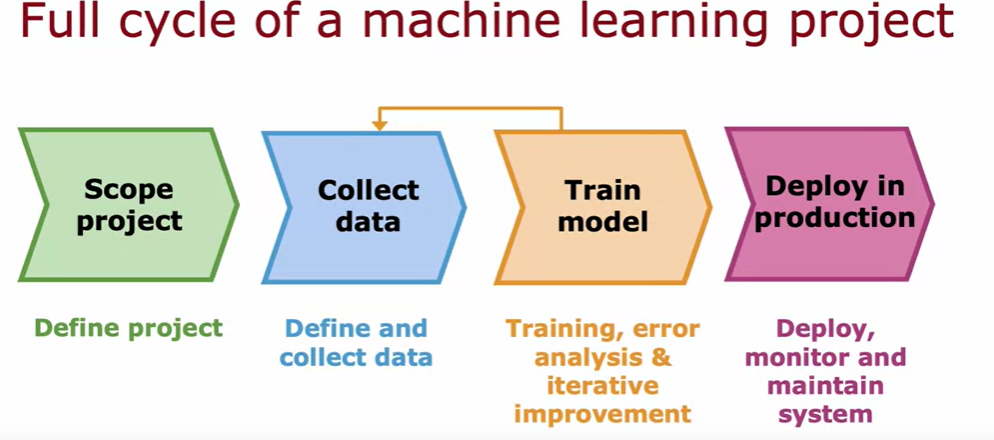
部署

一般采用部署服务器，API接口调用等方法实现

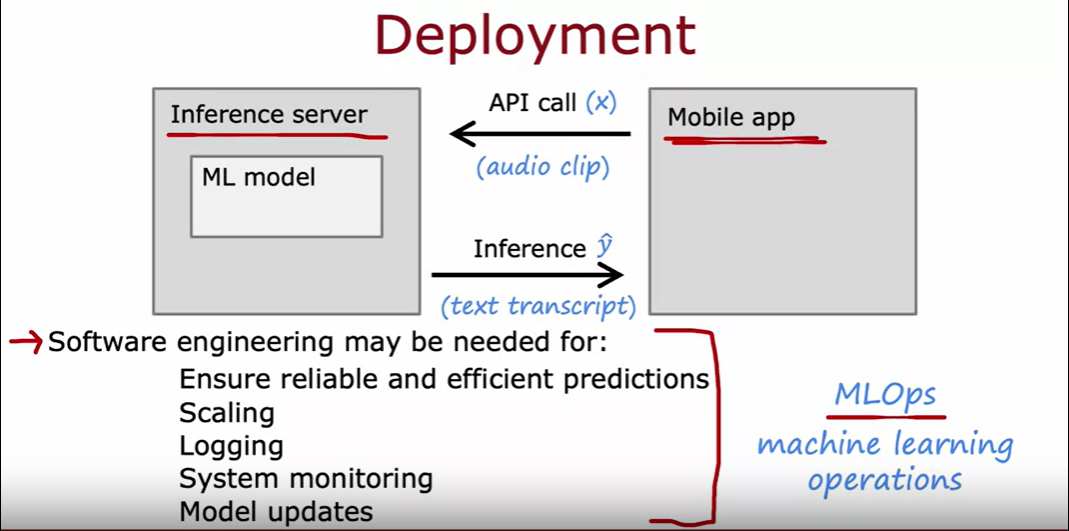
使用这种部署方式需要有一定的软件工程来维护，维护计算成本，记录访问数据，保证正常运行

同时也需要用新的数据或者发现的更优质，更大数量的数据来更新模型

系统的部署、监督与维护称为 MLOps (operations)

公平，偏见与道德

• 缓解计划 当出现问题的处理方法，一般是回退到已知的安全的版本
• 监督
• 审核
• 多元化

偏斜数据集

数据数量向某一些类别严重倾斜

对于严重偏斜的数据集，一般的评价指标例如准确率是排不上用场的

例如：千人中只有一人的患病率 在训练的模型中准确率达到99% 在一直输出不患病的算法中却可以达到99.9%的精度 但是两者究竟哪个更精确呢？后者的无意义性也没有通过指标表现出来

因此对于偏斜的数据集，要采用另外的评价指标

精确度与召回率

混淆矩阵

由交叉验证集的真实值与预测值组合而成的矩阵

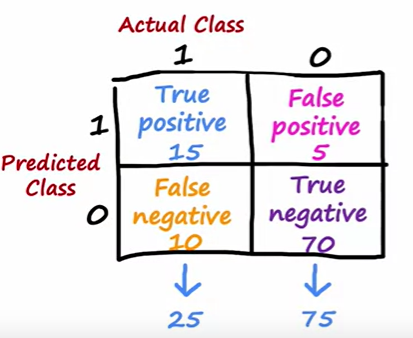
True positive 预测值与真实值都是1 False positive 预测值与真实值都是0 False negative 预测值与真实值不符且预测为1 True negative 预测值与真实值不符且预测为0

依此定义精确值与召回率

Precision

意为在预测的正值里有多少是对的

Recall

意为在正值的数据里有多少是被预测到的

可以理解为在正值数据集，一次召回可以找回多少正值数据

• 精度说明如果预测患者有病，那么其真的有病的概率

• 召回率说明如果患者有病，其被预测发现的概率

阈值选择

这两种指标一般要求都不错的高度

但一般会相互平衡

假设在进行分类

设定阈值为 0.9 ，如果阈值超过0.9，认为是 1，否则为0

在这样的关系下，显然精确度会高，因为当有很大把握才认为是 1 但是召回率就会很小，因为对于可能是1的没把握认为1

但是如果阈值为 0.1，情况就相反

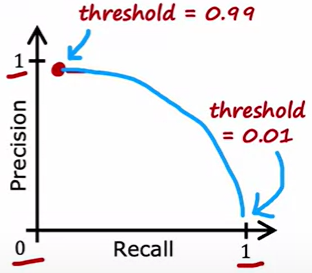
一般可以自己调整

F1 score

将精度与召回率结合到一个指标中，利于明确哪种平衡最优

F1 score 更关注较小值的函数

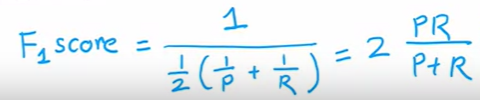
这个式子在数学中称为调和均值 (倒数平均数)