Abstract
重定义了学习函数,改为学习残差函数并构建了深层网络,击败VGG等一众模型
Motivation
深度模型训练很难:
- 梯度消失问题
- 正则化方法可以有效缓解
- 模型退化问题
- 目前训练中发现增加网络的深度反而精度有所下降,出现模型的退化现象,按理说更深的网络在理想情况下,可以在浅层保持一致的参数,在深层完全不学习,保持恒等映射,而不至于弱于浅层的网络,但实际上却是退化了
- 这说明深层模型在优化上存在问题,产生了训练误差
残差训练的思路:
- 残差学习并非突发奇想,在向量量化技术中,高维的向量的压缩,就需要很大的码本来保证较高的压缩精度,因此残差向量量化被提出,可以先用较小码本来压缩原始向量,然后将原始向量-近似向量,得到残差,这个残差有较小的范数(magnitude),更好被表示(方向上有更好的可预测性)
- 其余例如偏微分求解等也存在类似的思路
- 从残差角度上看,学习残差比学习一个完整的方程似乎更加简单,其往往更好表示,有更简单的结构或方向上有更强的预测性
Note
什么是向量量化?
这是一种数据压缩技术。
预先定义码本,其中有一组向量,对于一个输入的向量,在码本中找到最接近的向量来代替它,实现数据压缩
那不如让模型学习残差,而通过短接(shortcut)来保证模型可以保持之前的最优结果,但是之前的最优往往不是模型的最优,所以残差可以学习到一些扰动,来达到更优的结果
Method
Residual Learning
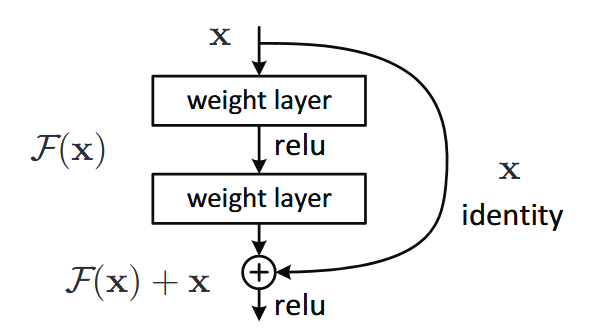
残差学习其实就是学习以下方程:
其中x是之前的输出,F代表层学习,之前的输出以直接逐元素相加的方式添加到当前层之中,维度不同用0填充,添加之后再进行激活,例如上图的学习为
文中还提到另一种残差连接:
其中,Ws是投影矩阵,通过1卷积实现,有两种作用:
- 保持维度相同
- 提供非线性的学习
论文中大量实验验证,实际上使用1卷积来实现维度对齐即可,其提供的非线性学习的增益和代价不成正比
Model
文中参考VGG,提出基础模型:
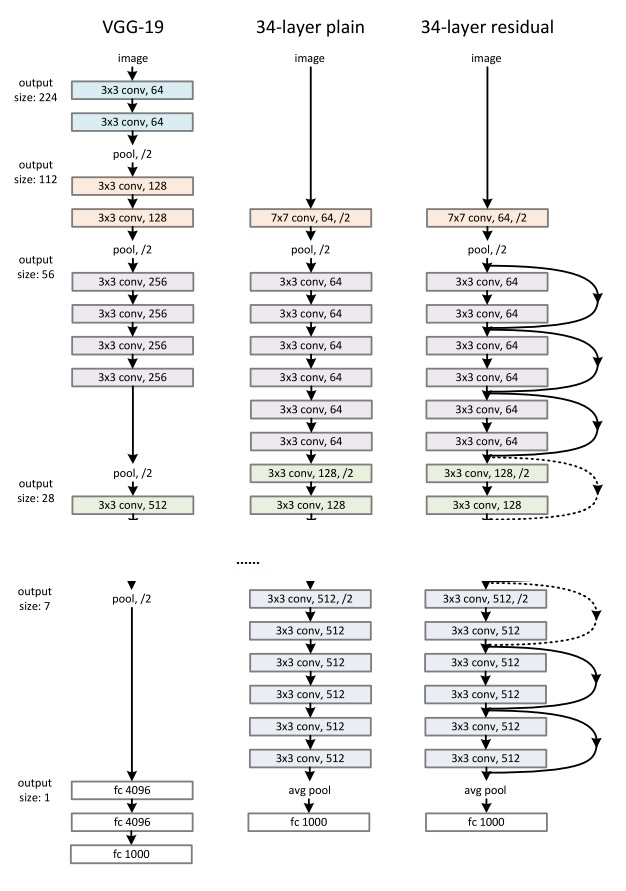
先用7卷积降维和学习,再用3卷积,逐步扩大通道数,最后平均池化后预测,文中提到没有使用Dropout等,有使用BN等其他技术,训练和测试方法参考AlexNet
同时,文中使用了两种卷积块
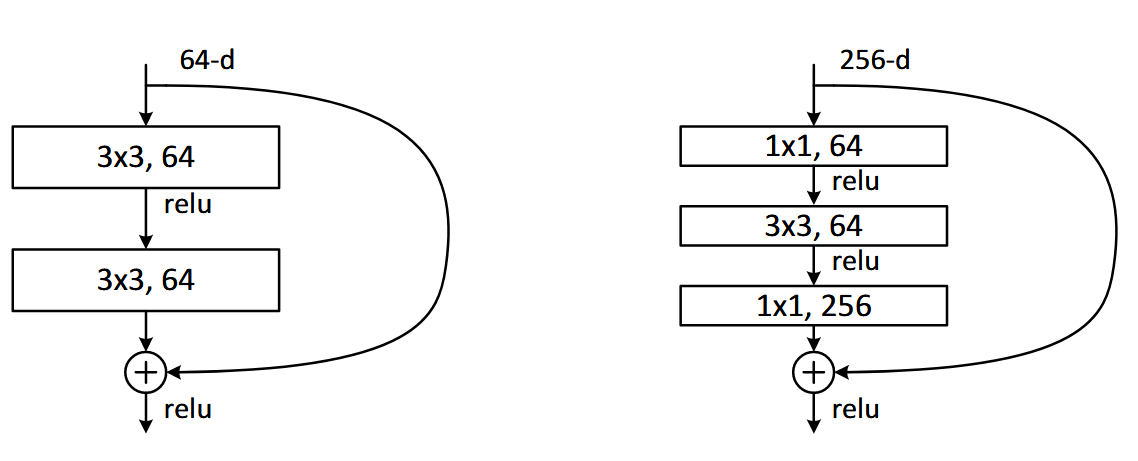
其中,左边是普通的卷积,用于浅层模型(18-34),右边是瓶颈层,使用1卷积来降低计算量,用于深层模型(50以上)
Experiments
训练细节:
- 随机放缩
- 随机翻转
- 填充并裁剪
- 像素归一化和颜色增强等
优化配置:
- batch szie 为256
- 学习率0.1,每次停止除以10
- weight decay 为1e-5,momentum为0.9
- 没有dropout
论文中做了大量的论证实验:
- 有无残差
- 如何残差
- 残差模型的泛化性(CIFAR-10)
- 模型深度
- 残差的响应(response)
- 等等
其中,得到一些较为关键的结论:
- 模型精度随深度提升,但是对比了1000层模型和100层模型后,发现精度下降,论文认为是因为复杂模型对小数据集存在过拟合,如果使用强正则化技术可能可以改善,但是也说明残差无法完美解决梯度问题
- 残差响应小,论文希望残差的学习是学习一些小的扰动,并做了一个测量response的实验,计算其标准差,发现确实response比较小,更靠近0,且越深越小,倾向于对每一层的信号进行更少的更改
Conclusion
ResNet提出的残差学习十分有效,确实是里程碑式的论文,论文分析模型深度退化的原因,并提出一个看似理所当然的点进行优化,十分简单但精妙的创新了网络学习的方式,经久不衰
尽管残差机制十分有效,但是实际上存在一些问题:
- 恒等映射保证了学习不退化,却无法保证得到最优解
- 特征也可能随映射而积累冗余,存在性能上的瓶颈
- 无法完全解决梯度问题
Refer
【笔记参考】ResNet 论文概览与精读 | 周弈帆的博客
【代码实现】