Diffusion Model Deep understanding

Before Reading

本文基本来自对大佬博客什么是扩散模型？ | Lil’Log --- What are Diffusion Models? | Lil’Log的翻译，大佬的文章面面俱到，对于如我这般的人来说实在有些晦涩，在学习MIT6.S184之后，对扩散终于有入门级别的理解，所以一半翻译一半整理，对其中部分理论进行更详细的解释和补充，同时也跳过了部分非理解重点的内容，后续的Flow Matching的理论在MIT课程的Note An Introduction to Flow Matching and Diffusion Models 中有详尽且通俗的解释

Before Learning

除了DM之外还有许多的生成模型，GAN、VAE和Flow-based模型，它们在生成高质量样本方面取得巨大成功，每种模型都有其自身的局限性。

• GAN模型对抗性训练的性质和潜在的训练不稳定性，生成多样性不足
• VAE依赖于代理损失(surrogate loss)
• 流模型必须使用专门的架构来构建可逆变换。

而扩散模型基于非平衡热力学知识(non-equilibrium thermodynamics)，定义一个马尔科夫链(Markov chain)，每一步慢慢的增加随机噪声，然后通过反向扩散过程来构造期望的采样分布

相比 VAE 和 Flow models，扩散模型学习的步骤确定，潜在变量维度更高（与原始数据相同）。

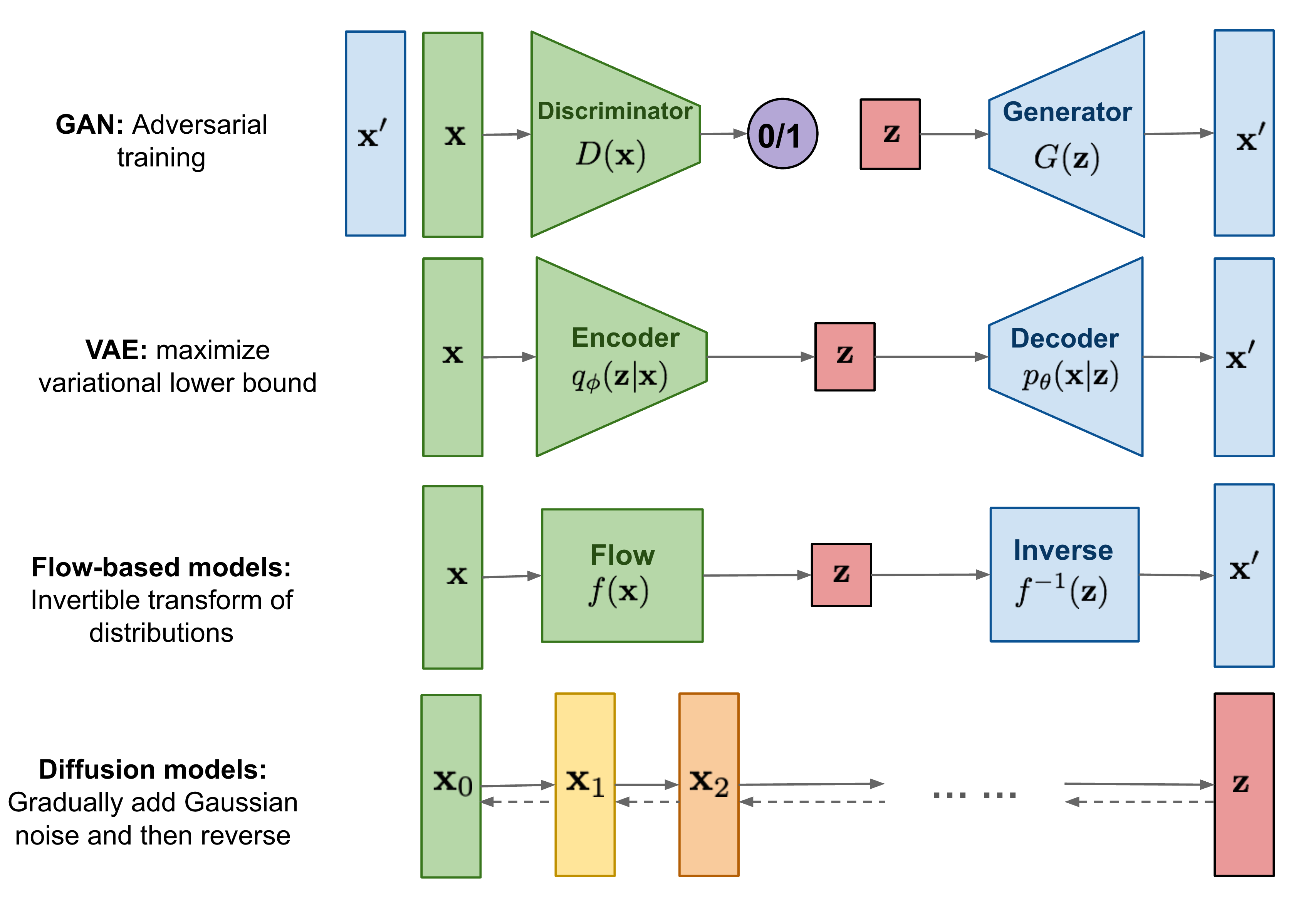
What are DMs

现有的扩散模型基于数个前人的伟大工作，扩散概率模型(diffusion probabilistic model) Sohl-Dickstein et al., 2015 ，噪声-条件评分网络(noise-conditioned score network) NCSN; Yang & Ermom, 2019 ，去噪扩散概率模型(denoising diffusion probabilistic modelDDPM; Ho et al. 2020

Forward Diffusion Process

给定一个从真实分布中采样的出来的样本点，每次对其增加一个微小的高斯噪声，持续 T 步，最后生成一个 $x_1\dots \dots x_T$ 的序列，

要从高斯分布里采样出来一个$z$，其公式如下：

$$\frac{z-\mu }{\sigma }\sim \mathcal{N}(0,I)$$

做一点变换（重采样）：

$$z=\mu +\sigma \cdot \epsilon \epsilon \sim \mathcal{N}(0,I)$$

Note

Why Doing Such a Change

因为直接从高斯分布里采样$z$的话不可微分，无法求导优化，所以希望能换一种可微分的方式，在VAE中提出，用一个固定噪声$\epsilon$来代替原分布，化简得到重采样式子

而对于每次加噪，公式是：

$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{\epsilon }_{t-1}$

其中，$\sqrt{1-{\beta }_t}{x}_{t-1}$ 是均值，$\sqrt{{\beta }_t}$ 是方差，所以在这个式子下，$x_t$ 会逐渐失去其可辨识性，会越来越接近高斯分布（参照上面的式子）

$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},({\beta }_t)I)$

这里其实隐含了$x_{t-1}$的系数和噪声系数的平方和为1的假设

对其进行化简，令${\alpha }_t=1-{\beta }_t\text{和}{\bar{\alpha }}_t={\prod }_{i=1}^t{\alpha }_i$ 可得

$$\begin{array}{rlr}{\mathbf{x}}_t& =\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{ϵ}}_{t-1}& ;\text{where }{\mathbf{ϵ}}_{t-1},{\mathbf{ϵ}}_{t-2},\cdots \sim \mathcal{N}(0,\mathbf{I})\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{\mathbf{x}}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{\mathbf{ϵ}}}_{t-2}& ;\text{where }{\overline{\mathbf{ϵ}}}_{t-2}\text{ merges two Gaussians (*).}\\ & =\cdots & \\ & =\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}\mathbf{ϵ}& \\ q({\mathbf{x}}_t|{\mathbf{x}}_0)& =\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I})& \end{array}$$

在高斯分布中，对于 $\mathcal{N}(0,{\sigma }_1^2\mathbf{I})$ + $\mathcal{N}(0,{\sigma }_2^2\mathbf{I})$ ，可以得到 $\mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)\mathbf{I})$

每次增加的噪声不一定一致，直观来看，对于原始图片，微量的噪声可以造成很大的影响，对于中间过程，微量噪声基本看不出来，如果这样来看，当样本变得嘈杂时，可以承受更大的步长。

Langevin dynamics

朗之万动力学(Langevin dynamics) 是一个物理概念，用于对分子系统做统计建模，结合随机梯度下降(stochastic gradient descent)构成 随机梯度下降朗之万动力学Welling & Teh 2011

提供了一种采样方法，使用Markov chain 更新中的梯度${\nabla }_{\mathbf{x}}\log p(\mathbf{x})$ 来生成概率密度 $p(x)$ 的样本

${\mathbf{x}}_t={\mathbf{x}}_{t-1}+\frac{\delta }{2}{\nabla }_{\mathbf{x}}\log p({\mathbf{x}}_{t-1})+\sqrt{\delta }{\mathbf{ϵ}}_t,\text{where }{\mathbf{ϵ}}_t\sim \mathcal{N}(0,\mathbf{I})$

对比标准的 SGD 方法，随机梯度朗之万方法将高斯噪声结合进参数更新中，避免陷入局部最优解

Note

Langevin dynamics

是一种考虑到系统热噪声下用来模拟分子运动的动力学公式，在机器学习中用来模拟从概率分布中抽取样本的过程

直观来看，其实这是在确定性上增加不确定性，沿梯度方向优化的同时增加噪声，让结果在高峰随机游走，避免局部最优

【概率方法】朗之万动力学 Langevin Dynamics-CSDN博客

Reverse diffusion process

如果逆转上述过程，并从 $q(x_{t-1}|x_t)$ 中取样，我们可以从高斯噪声输入中重新得到真实的样本，如果${\beta }_t$ 足够小，那么$q(x_{t-1}|x_t)$ 也将是高斯的

不幸的是，我们无法轻易估计$q(x_{t-1}|x_t)$ ，因为它需要使用到整个数据集，因此我们需要一个学习一个模型$p_{\theta }$ 来近似这些条件概率，以便运行反向扩散过程

$$p_{\theta }({\mathbf{x}}_{0:T})=p({\mathbf{x}}_T)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$

可以发现，当条件为 $x_0$ 的时候，也就是初始状态已知时，条件概率是可以计算的

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_{t-1};\tilde{\mathbf{\mu }}({\mathbf{x}}_t,{\mathbf{x}}_0),{\tilde{\beta }}_t\mathbf{I})$$

再依据贝叶斯公式，可以展开为：

$$\begin{array}{rl}q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)& =q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},{\mathbf{x}}_0\right)\frac{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0\right)}{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)}\\ & \propto \exp \left(-\frac{1}{2}\left(\frac{{\left({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}\right)}^2}{{\beta }_t}+\frac{{\left({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{{\left({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0\right)}^2}{1-{\bar{\alpha }}_t}\right)\right)\\ & =\exp \left(-\frac{1}{2}\left(\frac{{\mathbf{x}}_t^2-2\sqrt{{\alpha }_t}{\mathbf{x}}_t{\mathbf{x}}_{t-1}+{\alpha }_t{\mathbf{x}}_{t-1}^2}{{\beta }_t}+\frac{{\mathbf{x}}_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{\mathbf{x}}_{t-1}+{\bar{\alpha }}_{t-1}{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{{\left({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0\right)}^2}{1-{\bar{\alpha }}_t}\right)\right)\\ & =\exp \left(-\frac{1}{2}\left(\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right){\mathbf{x}}_{t-1}^2-\left(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right){\mathbf{x}}_{t-1}+C\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)\right)\right)\end{array}$$

其含义是 在$x_0,x_t$ 已知的条件下$x_{t-1}$成立的概率等于

• 在$x_0,x_t$成立下$x_{t-1}$成立的概率
• 乘以$x_0$成立下$x_t$成立 的情况中$x_{t-1}$成立的概率

我们希望条件概率的分布与高斯分布有关，于是建模成与某个高斯分布成正比，逐步拆开可以发现最后成为一项二次函数，也就是说满足高斯分布的性质，可以由二次函数的性质得到方差和均值，等于：

$$\begin{array}{rl}{\tilde{\beta }}_t& =1/\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)=1/\left(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}\right)=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ {\tilde{\mu }}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)& =\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right)/\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)\\ & =\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}$$

由于$x_t$等于$x_0$加上高斯噪声得到，所以反过来${\mathbf{x}}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t\right)$，代入到均值的计算中，可以得到

$$\begin{array}{rl}{\tilde{\mathbf{\mu }}}_t& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right)\end{array}$$

扩散模型的目标是生成图片是高质量的，与现实一致的，也就是说生成数据的分布要与现实分布尽可能相近，也就是说要最大化真实数据分布的似然

Note

Likelihood-based model

扩散过程是不可微的，无法直接通过构造优化函数来梯度下降优化，需要引入似然函数来间接求解

这类模型成为Likelihood-based model

这个步骤十分类似于VAE，可以同样采用变分下界来优化这个负对数似然

$$\begin{array}{rl}-\log p_{\theta }\left({\mathbf{x}}_0\right)& \le -\log p_{\theta }\left({\mathbf{x}}_0\right)+D_{\mathrm{KL}}\left(q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)\Vert p_{\theta }\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)\right);\text{KL散度非负性}\\ & =-\log p_{\theta }\left({\mathbf{x}}_0\right)+{\mathbb{E}}_{{\mathbf{x}}_{1:T}\sim q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)/p_{\theta }\left({\mathbf{x}}_0\right)}\right]\\ & =-\log p_{\theta }\left({\mathbf{x}}_0\right)+{\mathbb{E}}_q\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}+\log p_{\theta }\left({\mathbf{x}}_0\right)\right]\\ & ={\mathbb{E}}_q\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}\right]\\ \text{令 }{L}_{\mathrm{VLB}}& ={\mathbb{E}}_{q\left({\mathbf{x}}_{0:T}\right)}\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}\right]\ge -{\mathbb{E}}_{q\left({\mathbf{x}}_0\right)}\log p_{\theta }\left({\mathbf{x}}_0\right)\end{array}$$

利用KL散度的非负性，构造出目标的上界，其中 q 是前向的固定分布，p是逆向的联合分布，消去了对数似然项，得到了仅依赖于路径分布的期望表达式

化简结果，得到原始目标的下界，满足小于等于原来的目标式

同样的，用另一种方式也可以得到相同的推到结果

$$\begin{array}{rl}{L}_{\mathrm{CE}}& =-{\mathbb{E}}_{q\left({\mathbf{x}}_0\right)}\log p_{\theta }\left({\mathbf{x}}_0\right)\\ & =-{\mathbb{E}}_{q\left({\mathbf{x}}_0\right)}\log \left(\int p_{\theta }\left({\mathbf{x}}_{0:T}\right)d{\mathbf{x}}_{1:T}\right)\\ & =-{\mathbb{E}}_{q\left({\mathbf{x}}_0\right)}\log \left(\int q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)\frac{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}d{\mathbf{x}}_{1:T}\right)\\ & =-{\mathbb{E}}_{q\left({\mathbf{x}}_0\right)}\log \left({\mathbb{E}}_{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}\frac{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}\right)\\ & \le -{\mathbb{E}}_{q\left({\mathbf{x}}_{0:T}\right)}\log \frac{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}\\ & ={\mathbb{E}}_{q\left({\mathbf{x}}_{0:T}\right)}\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}\right]=L_{\mathrm{VLB}}\end{array}$$

式子中使用交叉熵作为目标函数，并通过 Jensen不等式（凸函数的均值不小于函数的均值） 来化简

为了使得式子计算起来更加方便，，通过 前向传播(q)的拆分 和 逆向传播贝叶斯 的引入，可以将目标式子重写成多个KL散度和熵的结合

$$\begin{array}{rl}{L}_{\mathrm{VLB}}& ={\mathbb{E}}_{q\left({\mathbf{x}}_{0:T}\right)}\left[\log \frac{q\left({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{0:T}\right)}\right]\\ & ={\mathbb{E}}_q\left[\log \frac{{\prod }_{t=1}^{T}q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)}{p_{\theta }\left({\mathbf{x}}_T\right){\prod }_{t=1}^T{p}_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p_{\theta }\left({\mathbf{x}}_T\right)+\sum _{t=1}^T\log \frac{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p_{\theta }\left({\mathbf{x}}_T\right)+\sum _{t=2}^T\log \frac{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}+\log \frac{q\left({\mathbf{x}}_1\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p_{\theta }\left({\mathbf{x}}_T\right)+\sum _{t=2}^T\log \left(\frac{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}\cdot \frac{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)}{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0\right)}\right)+\log \frac{q\left({\mathbf{x}}_1\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p_{\theta }\left({\mathbf{x}}_T\right)+\sum _{t=2}^T\log \frac{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}+\sum _{t=2}^T\log \frac{q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)}{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0\right)}+\log \frac{q\left({\mathbf{x}}_1\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)}\right]\\ & ={\mathbb{E}}_q\left[-\log p_{\theta }\left({\mathbf{x}}_T\right)+\sum _{t=2}^T\log \frac{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}+\log \frac{q\left({\mathbf{x}}_T\mid {\mathbf{x}}_0\right)}{q\left({\mathbf{x}}_1\mid {\mathbf{x}}_0\right)}+\log \frac{q\left({\mathbf{x}}_1\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)}\right]\\ & ={\mathbb{E}}_q\left[\log \frac{q\left({\mathbf{x}}_T\mid {\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_T\right)}+\sum _{t=2}^T\log \frac{q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)}{p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)}-\log p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)\right]\\ & ={\mathbb{E}}_q\left[\underset{L_T}{\underbrace{D_{\mathrm{KL}}\left(q\left({\mathbf{x}}_T\mid {\mathbf{x}}_0\right)\Vert p_{\theta }\left({\mathbf{x}}_T\right)\right)}}+\sum _{t=2}^T\underset{L_{t-1}}{\underbrace{D_{\mathrm{KL}}\left(q\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)\Vert p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)\right)}}-\log p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)\right]\end{array}$$

再重述如下：

$$\begin{array}{rl}{L}_{\mathrm{VLB}}& =L_T+L_{T-1}+\cdots +L_0\\ \text{where}{L}_T& =D_{\mathrm{KL}}\left(q\left({\mathbf{x}}_T\mid {\mathbf{x}}_0\right)\Vert p_{\theta }\left({\mathbf{x}}_T\right)\right)\\ L_t& =D_{\mathrm{KL}}\left(q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t+1},{\mathbf{x}}_0\right)\Vert p_{\theta }\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t+1}\right)\right)\text{for}1\le t\le T-1\\ L_0& =-\log p_{\theta }\left({\mathbf{x}}_0\mid {\mathbf{x}}_1\right)\end{array}$$

其中 KL散度每次比较的是两个高斯分布，可以求得闭式解，而终态$L_T$不用优化（q没有可学习参数），$L_0$可以使用模型（例如一个离散的解码器）来单独建模，即在明确模型的reverse概率分布的时候代入$X_1$和时间得到

Parameterization of $L_t$ for Trainging Loss

我们的目标是求扩散的逆向过程概率分布，在前向过程确定的时候，我们表述了前向过程高斯分布的均值和方差，其中二者做为我们设定的参数使用

我们得到

$$\begin{array}{rl}{\tilde{\beta }}_t& =1/\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)=1/\left(\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}\right)=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ {\tilde{\mu }}_t\left({\mathbf{x}}_t,{\mathbf{x}}_0\right)& =\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right)/\left(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}\right)\\ & =\left(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0\right)\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}$$

且可以进一步得到

$$\begin{array}{rl}{\tilde{\mathbf{\mu }}}_t& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_t)\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_t\right)\end{array}$$

这说明，在初始点确定的情况下，目标分布的方差其实可以由前向过程确定，而目标分布的均值则是由增加的高斯噪声确定

也就是说要做模型的训练，得到这个目标分布，其实就差预测当t和x确定时的噪声

$$\begin{array}{rl}{L}_t& ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{ϵ}}\left[\frac{1}{2\Vert {\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t){\Vert }_2}\Vert {\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)-{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t){\Vert }^2\right]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{ϵ}}\left[\frac{1}{2\Vert {\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t){\Vert }_2}{\Vert \frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_t\right)-\frac{1}{\sqrt{{\bar{\alpha }}_t}}\left({\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)\Vert }^2\right]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{ϵ}}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t){\Vert }_2}\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t){\Vert }^2\right]\\ & ={\mathbb{E}}_{{\mathbf{x}}_0,\mathbf{ϵ}}\left[\frac{(1-{\alpha }_t{)}^2}{2{\alpha }_t(1-{\bar{\alpha }}_t)\Vert {\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t){\Vert }_2}\Vert {\mathbf{ϵ}}_t-{\mathbf{ϵ}}_{\theta }(\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t,t){\Vert }^2\right]\end{array}$$

这是MSE（均方差），实际上外部的权重部分可以去掉，不影响最优解的位置

在训练得到均值表示后，通过逐步Xt的推导实现结果的生成

Connection with Noise-conditioned score Networks（NCSN）

在之后的文章中基于朗之万动力学引入分数函数${\nabla }_{\mathbf{x}}\log q(\mathbf{x})$， 这个函数作为噪声的补足项，实际上给出了概率分布的前进方向

引入这个之后，训练目标变成训练${\mathbf{s}}_{\theta }(\mathbf{x})\approx {\nabla }_{\mathbf{x}}\log q(\mathbf{x})$ ，称为score matching

Note

关于分数函数与噪声的另一种说法

实际上，基于流形假设，大部分数据集中在低维流形上，这意味着数据无法覆盖到整个空间，在数据密度低的区域，分数估计可靠性较低。在数据中添加高斯噪声，可以扰动数据分布覆盖整个空间，使得分数估计更加稳定

Parameterization

参数的设置会提高模型的性能，对于${\beta }_t$ ，通过基于余弦的变量有利于更加的性能

对于协方差矩阵，其实也是由${\beta }_t$来确定，或者可以通过模型确定，构建混合损失 ${\mathcal{L}}_{\text{hybrid}}={\mathcal{L}}_{\text{simple}}+\lambda {\mathcal{L}}_{\text{VLB}}$ ，其中将$\lambda$ 设置得很小，以此来减少对均值训练的影响，使其仅对协方差矩阵的学习有指导作用

Conditioned Generation

为了将类别信息融入扩散过程中，提出使用分类器$f_{\varphi }(y\mid {\mathbf{x}}_t,t)$ ，定义为给定x，t的情况下，得到向条件信息y（类别信息）的梯度，引导扩散过程

这实际上就是引入了${\nabla }_{{\mathbf{x}}_t}\log q(y\mid {\mathbf{x}}_t)$ ，再加上之前噪声预测实际上变成对分数函数 ${\nabla }_{{\mathbf{x}}_t}\log q({\mathbf{x}}_t)$ 的预测，可以得到一个二者的联合分布，将最终的噪声预测变成

$${\overline{\mathbf{ϵ}}}_{\theta }({\mathbf{x}}_t,t)={\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)-\sqrt{1-{\bar{\alpha }}_t}w{\nabla }_{{\mathbf{x}}_t}\log f_{\varphi }(y\mid {\mathbf{x}}_t)$$

其中，$\omega$ 是调节分类引导的权重

Classifier-Free Guidance

我们可以进一步对分类器做简化，来实现只训练一个目标，通过贝叶斯和对数性质可以得到

$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log p(y\mid {\mathbf{x}}_t)& ={\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t\mid y)-{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t)\\ & =-\frac{1}{\sqrt{1-{\bar{\alpha }}_t}}\left({\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)\\ {\overline{\mathbf{ϵ}}}_{\theta }({\mathbf{x}}_t,t,y)& ={\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)-\sqrt{1-{\bar{\alpha }}_t}w{\nabla }_{{\mathbf{x}}_t}\log p(y\mid {\mathbf{x}}_t)\\ & ={\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)+w\left({\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\right)\\ & =(w+1){\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t,y)-w{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)\end{array}$$

其中，原本的分类器可以被两个分数估计器取代，也就可以被两个噪声预测取代，而这两个噪声预测时期上只有有无条件y的区别，也就是可以训练一个包含条件y的预测，并在训练的时候将y概率性的设置成空值，则可以实现只训练一个模型

Speed up Diffusion Models

扩散模型的训练非常慢，加速一直是其主要课题

DDIM; Song et al., 2020提出，扩散逆向过程实际上可以是一个非马尔可夫链过程，可以有确定性的采样，也就是ODE（常微分方程），传统的扩散是一种SDE（随机微分方程），这两者的区别就是是否有在方程中增加一个随机噪声，这也决定了两者是否是有确定解的

当DDIM证明了逆向过程可以是ODE的，因为具确定性，其采样速度可以快很多，不必采样全部的时间步，可以加入更多的嵌入信息

Note

DDPM & DDIM

二者是SDE和ODE的差别

在重参数化（Reparameterization）技巧后，扩散从实际上预测$p(x_{t-1}|x_t)$分布的均值和方差，变成预测噪声，并于$x_t$一起代入公式得到分布的均值，间接的预测分布

其中对于分布的方差，在DDPM（SDE）过程，实际上被设置成一个固定值${\sigma }_t^2\mathbf{I}$，即给定一个噪声系数${\sigma }_t$，这个系数由参数$\beta$确定，不过有些DDPM模型确实会预测方差

而对于DDIM（ODE）过程，由于是确定性的，其目标分布不依赖于方差项，所以不用考虑方差

Progressive Distillation(Salimans & Ho, 2022)

渐进式蒸馏，将训练好的确定性的采样器（模型）作为教师模型蒸馏成采样步数减半的学生模型，渐进式的递减

Consisteny Models (Song et al. 2023)

一致性模型，学习将扩散采样过程的任何中间数据点直接映射到原始数据：

Consistency Distillation

• 将扩散模型蒸馏成一致性模型，采样成本大大降低
• 通过最小化中间过程对最终结果之间的生成差异，希望学生模型可以在任何时间点都一步预测出最终结果，所以其损失是

$$\begin{array}{rl}{\mathcal{L}}_{\text{CD}}^N(\theta ,{\theta }^{-};\varphi )& =\mathbb{E}\left[\lambda (t_n)d(f_{\theta }({\mathbf{x}}_{t_{n+1}},t_{n+1}),f_{{\theta }^{-}}({\hat{\mathbf{x}}}_{t_n}^{\varphi },t_n))\right]\\ {\hat{\mathbf{x}}}_{t_n}^{\varphi }& ={\mathbf{x}}_{t_{n+1}}-(t_n-t_{n+1})\mathbf{\Phi }({\mathbf{x}}_{t_{n+1}},t_{n+1};\varphi )\end{array}$$

其含义是学生模型$\theta$ 在更远处预测最终结果等于教师模型${\theta }^{-}$在近处的最终预测结果

Consistency Training

类似于一致性蒸馏，只是从头开始训练而不是先有一个预训练模型，其损失是

$${\mathcal{L}}_{\text{CT}}^N(\theta ,{\theta }^{-};\varphi )=\mathbb{E}[\lambda (t_n)d(f_{\theta }(\mathbf{x}+t_{n+1}\mathbf{z},t_{n+1}),f_{{\theta }^{-}}(\mathbf{x}+t_n\mathbf{z},t_n))]\text{ where }\mathbf{z}\in \mathcal{N}(0,\mathbf{I})$$

x是原始数据点，z是噪声，${\theta }^{-}$是$\theta$的EMA(Exponential Moving Average)版本

含义是远点最终生成与近点都最终生成结果应该一致，由于没有预训练模型所以从 x开始加时间步长倍数的噪声

Note

EMA(Exponential Moving Average)

指数移动平均，或者称为影子权重（Shadow Weights）

也就是$\theta$的历史更新过程中平滑、累积的平均值

Latent Variable Space

潜在扩散模型（LDM; Rombach & Blattmann, et al. 2022），在潜在空间而不是像素空间做扩散，降低了训练成本提高推理速度，其认为图像的特征大部分是感知细节，例如语义等概念信息

LDM通过AutoEncoder学习深层特征，在特征嵌入上通过扩散过程生成语义概念

其实使用了两种正则化方法

• KL-reg：对学习到的潜在变量施加一个KL惩罚，使其接近标准正态分布
• VQ-reg：在decoder中使用矢量量化层（vector quantization）

LDM还使用了一种交叉注意力机制，将不同的额外信息通过各自的encoder得到嵌入后做交交叉注意力计算，引入不同模态来生成结果，最后在decoder中得到图像

Scale up Generation Resolution and Quality

在扩散的实际应用中，图像增强方法不可忽视，其中 Ho et al. (2021)提出噪声增强的方法，用于提高生成质量

其发现：

• 训练时，低分辨率时应用高斯噪声，高分辨时做高斯模糊有助于得到更好的增强结果

另外，unCLIP (Ramesh et al. 2022)的工作提出两阶段的扩散，实现条件生成

其中，左侧的文本encoder来自CLIP，生成文本嵌入，右上侧的encoder可以提供图像的风格等嵌入，来调整生成结果，最后的扩散decoder基于两个先验生成最终结果

此外，在工作Imagen (Saharia et al. 2022)中，提到应用无分类引导时，增加$\omega$ 有利于图像-文本对齐，但是保真度会变差，这是由于训练数据的x与预测值的范围不匹配造成的，加权求和导致预测结果与原始噪声不在一个范围内，可以进行阈值裁剪

Feature

流匹配（Flow Matching）和分数匹配（Score Matching）实际上在理论上整合了扩散模型的原理，提供一种更合理的训练和预测

其从理论上说明初始分布确定时，可以通过SDE和ODE构建随机性或确定性的采样过程，在形式和训练上更简单

其基本原理参考[2506.02070] An Introduction to Flow Matching and Diffusion Models

Refer

• 大佬的博客 什么是扩散模型？ | Lil’Log --- What are Diffusion Models? | Lil’Log
• 大佬的课 https://diffusion.csail.mit.edu/
• 文中出现的文献