降维与度量学习

样本的特征数称为 维数 ，当维数非常大时，称为维数灾难，在高维情形下，数据样本之间十分稀疏，因此要满足训练样本为密采样的总体样本数目的需求遥不可及，且距离的计算十分复杂，运算复杂度高

除了SVM的低维计算来表示高维情况，一般缓解高维灾难的方式是降维，通过某数学变换将原始高维空间转变到一个低维空间。此时样本密度大幅提高，距离计算简单，而且，降维不一定百分百丢失重要数据，而是可能去除了冗余，相似的多余属性等

K近邻学习

简单来说就是给定某个样本，KNN基于某种距离度量在训练集中找到与其距离最近的k个真实标记训练样本，然后基于k个邻居的真实标记进行预测

KNN分类

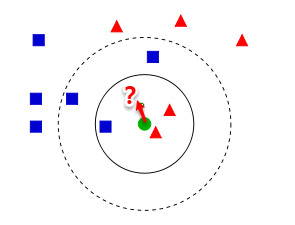
实际方法：

• 如果是k=3，那么离绿色点最近的有两个红色的一个蓝色的，所以绿色点属于红色
• 如果k=5，离绿色点最近的有三个蓝色的，两个红色的，所以绿色点属于蓝色

这种监督学习方法没有显式的训练过程，当有新样本才开始做计算和预测，被称为懒惰学习方法。

朴素贝叶斯的训练过程就是参数估计，实际上也可以懒惰式学习

这类方法在训练阶段的开销基本为0，另外一些方法被称为急切学习，一有数据就开始训练，绝大多数已学的方法都是后者

总结：

• KNN算法核心在于k值的选取和距离的度量
• k值太小，会有噪声干扰
• k值太大，预测能力减弱（分的细粒度不够）

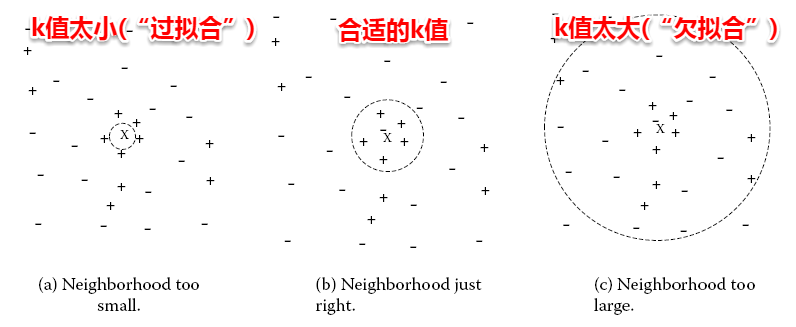
一般要通过某种方法选定k值，常见的是交叉验证法。另外，对于不同的度量方法也会影响k值的选定，常见的有闵可夫斯基距离，曼哈顿距离，VDM等

Note

KNN的距离度量需要根据样本的性质来选择，同时要注意去量纲、归一化等，消除大量纲或大数据的影响。

MDS算法

无论是升维（核函数）还是降维（数据降维），都希望原始空间样本点之间的距离在新空间基本保持不变，才不会使得原始空间样本之间的关系及总体分布发生较大的变化，多维缩放（MDS） 秉承这一观点，要求原始空间样本之间的距离在降维后的低维空间得以保持

假设有距离矩阵$D\in {\mathbb{R}}^{m\times m}$，降维之后的低维表示 $Z\in {\mathbb{R}}^{d\times m}$ ，$B=Z^{T}Z$ 为内积矩阵，那么：

$$\begin{array}{rl}dis{t}_{ij}^2& =\Vert z_i{\Vert }^2+\Vert z_j{\Vert }^2-2z_i^{\mathrm{T}}{z}_j\\ & =b_{ii}+b_{jj}-2b_{ij}.\text{(1)}\end{array}$$

将低维表示Z去中心化，也就是每个样本向量都减去样本集的均值向量，也就是样本向量求和之后等于零向量

依据内积计算原理，矩阵B的每一列及每一行求和都是零向量（因为求和之后提公因子后，等于每一列相加乘上一个公因子，而列相加之和为零向量）

这样，可以得到式子如下：

$$\begin{array}{rl}\sum _{i=1}^{m}dis{t}_{ij}^2& =\mathrm{tr}(\mathbf{B})+m{b}_{jj}\text{(2)}\ast 1/m\\ \sum _{j=1}^{m}dis{t}_{ij}^2& =\mathrm{tr}(\mathbf{B})+m{b}_{ii}\text{(3)}\ast 1/m\\ \sum _{i=1}^m\sum _{j=1}^{m}dis{t}_{ij}^2& =2m\mathrm{tr}(\mathbf{B})\text{(4)}\ast 1/(m^2)\end{array}$$

根据式子(1)-(4)，可以化简得到每一个 $b_{ij}$

即 $b_{ij}=(1)-(2)(1/m)-(3)(1/m)+(4)(1/m^2)$ ，再对B进行特征值分解得到Z（实际上是得到特征值和特征向量，B的特征值和特征向量与Z的是平方关系）

PCA

不同于MDS的距离保持，PCA希望通过线性变换来将原始空间中的样本投影到新的低维空间中。

采用一组新的基表示样本点，每个基向量都是原来基向量的线性组合，通过使用尽可能少的新基向量来表示样本，从而实现降维

实际上是将样本投影到某个由新的基向量确定的超平面（舍弃一些维度），最理想的情形是：样本点都能在超平面上表示且这些表示能很好的分散开来，但是一般做不到，只要求两种性质可以成立：

• 最近重构性 样本点到超平面的距离足够近，尽可能在超平面附近
• 最大可分性 样本点在超平面的投影分散开，即坐标具有可分性

这两种性质在本质上确实同有一个优化的目标函数

$$\begin{array}{rl}& \min \sum _{i=1}^m{\Vert \sum _{j=1}^{d^{\prime }}{z}_{ij}{w}_j-x_i\Vert }_2^2=\sum _{i=1}^m\Vert z_i^{\mathrm{T}}{z}_i{\Vert }^2-2\sum _{i=1}^m{z}_i^{\mathrm{T}}{\mathbf{W}}^{\mathrm{T}}{x}_i+\mathrm{const}\\ & \\ & \underset{\mathbf{W}}{\min }-\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}\left(\sum _{i=1}^m{x}_i{x}_i^{\mathrm{T}}\right)\mathbf{W}\right)\\ & \\ & \underset{\mathbf{W}}{\max }\mathrm{tr}({\mathbf{W}}^{\mathrm{T}}\mathbf{X}{\mathbf{X}}^{\mathrm{T}}\mathbf{W})\\ & s.t.{\mathbf{W}}^{\mathrm{T}}\mathbf{W}=\mathbf{I},\end{array}$$

其中，最大重构性要求优化第二条公式，最大可分性要求优化最后一条公式，这本质上是一致的

可以用拉格朗日乘子法求解上述优化

$X{X}^{T}W=\lambda W$

因此只需要对X（中心化）协方差矩阵特征值分解就可以得到W（上述为特征值公式$Ax=\lambda x$)

核化线性降维

核技巧在SVM中使用广泛，这本身是一种十分巧妙的技巧。用低维的核函数内积来映射高维的内积运算，就完全不需要关注高维的特征向量如何计算。将无限维的空间求解问题，变成在样本空间的求解问题

在核化线性降维中，为了将在低维空间纠缠在一起的非线性数据分开，先将样本映射到高维空间，再在高维空间中使用线性降维方法。

尽管我们自己定义了核函数，却难以明确核函数将样本映射到高维空间的具体映射规则，而只知道计算高维空间的样本内积。

为将问题转换成可以用已知方法解决的问题，提出：空间中任一向量，都可由空间中所有的样本线性表示

$$\begin{array}{rl}& \left(\sum _{i=1}^m{z}_i{z}_i^T\right)\mathbf{W}=\lambda \mathbf{W}\\ & \mathbf{W}=\frac{1}{\lambda }\left(\sum _{i=1}^m{z}_i{z}_i^T\right)\mathbf{W}=\sum _{i=1}^m{z}_i\frac{z_i^T\mathbf{W}}{\lambda }\\ & =\sum _{i=1}^m{z}_i{\alpha }_i\end{array}$$

其中，W是高维空间的基向量（特征向量），Z是高维坐标表示。其中 $z_i^{T}W$ 是向量内积，结果是一个常数，除以 $\lambda$ 也是一个常数，也就是说 W 实际上可以通过高维空间中的样本坐标向量的线性计算来表示

这样一来，主成分（特征向量）W可以通过高维表示Z来表示而高维表示Z的内积可以通过低维表示的内积的核函数来表示，这就打通了高维-低维的通道，利用核函数技巧实现高维运算

$$\begin{array}{rl}\Phi (X)\Phi (X{)}^T{\mathbf{w}}_i& ={\lambda }_i{\mathbf{w}}_i\\ {\mathbf{w}}_i& =\sum _{k=1}^N{\alpha }_i\Phi \left({\mathbf{x}}_i\right)=\Phi (X)\mathbf{\alpha }\\ \Phi (X)\Phi (X{)}^T\Phi (X)\mathbf{\alpha }& ={\lambda }_i\Phi (X)\mathbf{\alpha }\\ \Phi (X{)}^T\Phi (X)\Phi (X{)}^T\Phi (X)\mathbf{\alpha }& ={\lambda }_i\Phi (X{)}^T\Phi (X)\mathbf{\alpha }\end{array}$$

将核函数矩阵$\Phi (X{)}^T\Phi (X)$定义为K，可得

$$\begin{array}{rl}{K}^2\mathbf{\alpha }& ={\lambda }_{i}K\mathbf{\alpha }\\ K\mathbf{\alpha }& ={\lambda }_i\mathbf{\alpha }\end{array}$$

也就将问题化简为对和矩阵K的特征分解，进行PCA就是选取前k个特征值与特征向量

具体为，例如选取了K个主成分，那么：

$$\begin{array}{rl}{\hat{\mathbf{x}}}_{new}& ={\mathbf{w}}_j^T{\mathbf{x}}_{new}\\ & ={\left(\sum _{i=1}^N\Phi ({\mathbf{x}}_i){\alpha }_i\right)}^T\Phi ({\mathbf{x}}_{new})\\ & =(\Phi (X)\mathbf{\alpha }{)}^T\Phi ({\mathbf{x}}_{new})\\ & ={\mathbf{\alpha }}^T\Phi (X{)}^T\Phi ({\mathbf{x}}_{new})\\ & =[{\alpha }_1,\dots ,{\alpha }_N][k({\mathbf{x}}_1,{\mathbf{x}}_{new}),\dots ,k({\mathbf{x}}_N,{\mathbf{x}}_{new}){]}^T\end{array}$$

其中用K个主成分就遍历K次，每次用不同的w

流形学习

流形学习(manifold learning)是一种借助拓扑流形概念的降维方法，流形是指在局部与欧式空间同胚的空间，局部与欧式空间具有相同的性质，用欧式距离计算样本之间的距离。

这样即使高维空间的分布十分复杂，局部上依然满足欧式空间的性质，基于流形学习的降维正是这种”领域保持“的思想，等度量映射（lsomap） 试图在降维前后保持领域内样本之间的距离，而局部线性嵌入（LLE） 则是保持领域内样本之间的线性关系

Note

什么是流形？

大概可以看成是一个弯曲、卷起来的、光滑的表面

例如地球表面，在全局看起来是弯曲的，但是局部是平面。虽然说数据分布在一个高维空间中，在流形学习的假设中，认为数据并非杂乱无章的分布在空间，而是紧密的分布在一个低维流形

什么是同胚？

描述拓扑学上的相同，例如甜甜圈和咖啡杯都有且只有一个洞，有某些方法可以将甜甜圈变成一个咖啡杯，同时不涉及到撕裂、粘合，只有拉伸、弯曲、挤压和扭曲操作，在这种操作下，如果A可以变成B，那么就说二者是同胚的

Tip

流形经典例子：瑞士卷

瑞士卷上的各个点分布在三维空间中，但是实际上将其展开之后分布在一个二维空间中，各个点之间其实能够保持邻居关系

等度量映射

高维空间中直线距离具有误导性，因为高维空间中的直线距离在低维空间中是不可达的，因此利用流形在局部上与欧式空间同胚的性质，可以使用近邻距离来逼近测地线距离，即对于一个样本点，它与近邻内的样本点之间是可达的，且距离使用欧式距离计算，这样样本空间就形成一张近邻图，高维空间中两个样本之间的距离就转为最短路径问题，可以用Dijkstra算法或Floyd算法计算最短距离，的得到高维空间中任意两点之间的距离后，可以使用MDS算法来计算器低维空间中的坐标

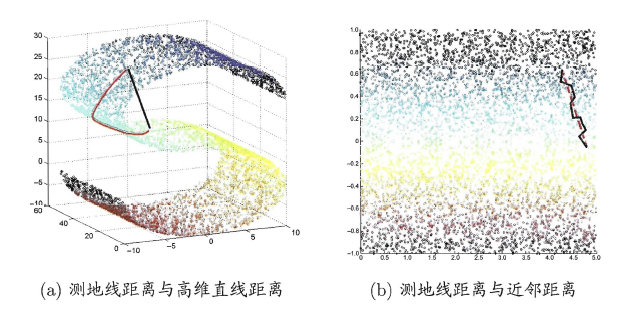
红线为测地线距离，黑线为高维距离，当空间中形成近邻图时，点与点之间的连线更接近实际的测地线距离

MDS方法先求出了低维空间的内积矩阵B，再计算出Z，但是没有得到一个B到Z的投影向量，因此对于新的样本无法直接计算其低维表示，书中利用已知高/低维度坐标的样本可以训练出一个投影器，用高维预测低维

对于近邻图的构建：

• 指定近邻个数
• 指定邻域半径

若领域范围过大，会造成短路，若过小，会造成断路

局部线性嵌入(LLE)

不同于lsomap算法去保持领域距离，LLE算法试图去保持领域内的线性关系，假定样本可以通过其邻域样本线性表出

$${\mathbf{x}}_i=w_{ij}{\mathbf{x}}_j+w_{ik}{\mathbf{x}}_k+w_{il}{\mathbf{x}}_l$$

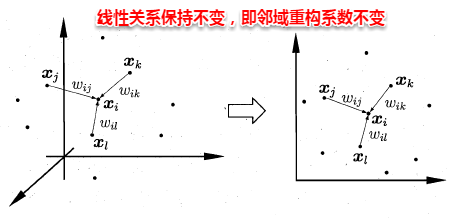
LLE算法：

• 首先根据近邻关系计算出样本的邻域重构系数w

$$\begin{array}{rl}& \underset{{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_m}{\min }\sum _{i=1}^m{\Vert {\mathbf{x}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{x}}_j\Vert }_2^2\\ & \text{ s.t. }\sum _{j\in Q_i}{w}_{ij}=1,\\ & \text{其中}{x}_i,x_j\text{均已知，令}{C}_{jk}=(x_i-x_j{)}^T(x_i-x_k).,w_{ij}\text{有闭式解}\\ & w_{ij}=\frac{{\sum }_{k\in Q_i}{C}_{jk}^{-1}}{{\sum }_{l,s\in Q_i}{C}_{ls}^{-1}}\end{array}$$

• 根据邻域重构系数不变的性质，求低维坐标

$$\begin{array}{rl}\underset{{\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_m}{\min }& \sum _{i=1}^m{\Vert {\mathbf{z}}_i-\sum _{j\in Q_i}{w}_{ij}{\mathbf{z}}_j\Vert }_2^2\\ \diamond & \mathbf{Z}=\left({\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_m\right)\in {\mathbb{R}}^{d^{\prime }\times m},(\mathbf{W}{)}_{ij}=w_{ij}\\ & \mathbf{M}=(\mathbf{I}-\mathbf{W}{)}^T(\mathbf{I}-\mathbf{W})\end{array}$$

最后利用矩阵M，优化问题重写：

$$\begin{gathered} \underset{\mathbf{Z}}{\min }\mathrm{tr}(\mathbf{ZM}{\mathbf{Z}}^T) \\ \text{s.t.}{\mathbf{ZZ}}^T=\mathbf{I}. \end{gathered}$$

Z由d个最小的特征值对应的特征向量组成

度量学习

之前的算法是先降维再计算距离，度量学习则是直接学习低维空间的距离

这需要定义一个合适的距离：

$$\begin{array}{rl}{\mathrm{dist}}_{\text{wed}}^2({\mathbf{x}}_i,{\mathbf{x}}_j)& =\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }_2^2\\ & =w_1\cdot {\mathrm{dist}}_{ij,1}^2+w_2\cdot {\mathrm{dist}}_{ij,2}^2+\dots +w_d\cdot {\mathrm{dist}}_{ij,d}^2\\ & =({\mathbf{x}}_i-{\mathbf{x}}_j{)}^T\mathbf{W}({\mathbf{x}}_i-{\mathbf{x}}_j)\end{array}$$

但是属性之间往往有关联，不能单独计算，引入马氏距离

$${\mathrm{dist}}_{\mathrm{mah}}^2({\mathbf{x}}_i,{\mathbf{x}}_j)=({\mathbf{x}}_i-{\mathbf{x}}_j{)}^T\mathbf{M}({\mathbf{x}}_i-{\mathbf{x}}_j)=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }_{\mathbf{M}}^2$$

其中，M是协方差矩阵的逆，这是一种考虑属性之间且无量纲

M又称度量矩阵，为保证距离度量的非负性和对成型，M必须为（半）正定对称矩阵，度量学习就是对度量矩阵进行学习，此时需要一个目标优化函数，在此不再赘述

Refer

西瓜书学习笔记(11)—降维与度量学习 - Heywhale.com