EM算法

Expectation-Maximization 期望最大化

常用的估计参数隐变量的利器，期望最大算法，是数据挖掘的十大经典算法

EM算法应用于训练集样本不完整即存在隐变量情形，通过两步走策略较好的估计隐变量的值

EM算法思想

实际上是一种迭代方法，若样本服从分布参数$\theta$ 已知，则可以根据观测的训练样本推断出隐变量Z的期望值（E步），若Z的值已知则运用最大似然估计出新的$\theta$值（M步），重复这个过程直到Z和$\theta$不变

简单来说：A和B参数，在开始状态下二者未知，知道了A就可以推断出B，知道了B就能知道A，可以考虑赋予A某种初值，得到B的估计值，从B当前值出发，重新估计A的取值，一直持续到收敛

• $\theta$ 推断隐变量Z的期望，记为$Z^t$
• 已观测变量X和$Z^t$ 对参数$\theta$ ，做极大似然估计，记为${\theta }^{t+1}$

聚类代表算法K-means：先选择类中心 → 样本划分到类簇 → 重新计算类中心 → 直到收敛，这个过程和EM迭代方法及其相似，样本类别看作隐变量Z，类中心看作样本的分布参数$\theta$，K-means就是通过EM算法来进行迭代，不同的是，K-means目标是最小化样本点到对应类中心距离和，上述为极大化似然函数

EM算法数学推导

对于似然函数见极大似然估计

样本属性值已知，可以通过极大化对数似然，对每个参数求偏导来计算得到参数的值（最大化似然函数），但是存在隐变量时，无法直接求解，通常最大化一观测数据的对数“边际似然(marginal likelihood)“来将隐变量引入其中

$$LL(\Theta |\mathbf{X})=\ln P(\mathbf{X}|\Theta )=\ln \sum _{\mathbf{Z}}P(\mathbf{X},\mathbf{Z}|\Theta )$$

其中，Z是隐变量，对于参数估计，目前问题变成找到两个变量取值，使得目标函数最大，可以通过偏导来实现

但是和的对数求导复杂，此时需要引入Jensen不等式来简化表达式

其中，由于对数函数是凹函数，可以将“和的对数”转变为“对数的和”，也就是说利用Jensen不等式，将对数放到加和符号之中，就可以得到

$$\begin{array}{rlr}\sum _i\log p(x^{(i)};\theta )& =\sum _i\log \sum _{z^{(i)}}p(x^{(i)},z^{(i)};\theta )& \text{(1)}\\ L(\theta )& =\sum _i\log \sum _{z^{(i)}}{Q}_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}& \text{(2)}\\ J(\theta ,Q)& \ge \sum _i\sum _{z^{(i)}}{Q}_i(z^{(i)})\log \frac{p(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}& \text{(3)}\end{array}$$

其中，$Q_i$ 是一个概率分布，实际上引入$Q_i$ 之后，对数中的式子就像是一个期望的形式（概率 $\times$ 取值），又满足凹函数，可以利用Jensen不等式将对数放到加和之中

接下来先固定 $\theta$ ,求解Q使得$J(\theta ,Q)$ 在 $\theta$ 处与 $L(\theta )$ 相等，即求出 $L(\theta )$ 的下界，再固定 Q，调整$\theta$ ，最大化下界 $J(\theta ,Q)$ ，不断重复两个步骤直到稳定

这个过程中，$Q$ 的计算公式实际上就是Z的后验概率

$$\begin{array}{rl}{Q}_i(z^{(i)})& =\frac{p(x^{(i)},z^{(i)};\theta )}{{\sum }_{z}p(x^{(i)},z;\theta )}\\ & =\frac{p(x^{(i)},z^{(i)};\theta )}{p(x^{(i)};\theta )}\\ & =p(z^{(i)}|x^{(i)};\theta )\end{array}$$

这个过程实际就是EM算法的E步（通过Jensen不等式，固定$\theta$计算下界，计算概率），M步（固定Q，计算 $\theta$ 最大化下界），从而不断推高边缘似然$L(\theta )$，从而计算出 $L(\theta )$ 取得极大值时隐变量Z的估计值

EM算法可以看作一种 坐标下降法，首先固定一个值，对另一个值求极值，不断重复到收敛

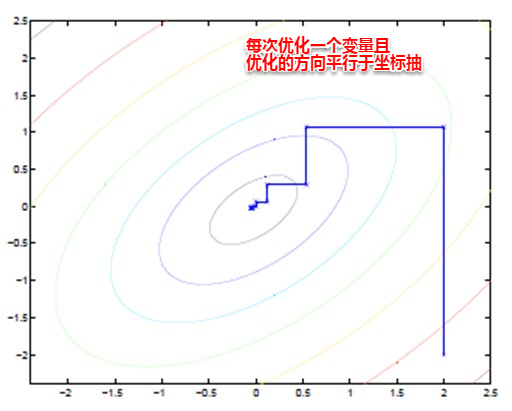
EM算法流程

1. E步，根据参数初始值或上一次的迭代模型参数计算出隐形变量的后验概率，其实就是隐形变量的期望，作为隐藏变量的现估计值：

$$Q_i(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta ).$$

2. 将似然函数最大化以获得新的参数值

$$\theta :=\arg \underset{\theta }{\max }\sum _i\sum _{z^{(i)}}{Q}_i(z^{(i)})\log \frac{p(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}$$

Refer

西瓜书学习笔记(8)—EM算法 - Heywhale.com