Supervised Learning

AGI

Artificial General Intelligence 通用人工智能

Supervised learning

监督学习

概念

根据输入的 x (input) 映射想要的 y (ouput) 结果，数据有标签

• 数据集 dataset
• 输入变量 (特征 feature) x
• 输出变量 (目标变量) y
• 预测变量 $\hat{y}$
• 误差 error 模型通过训练产生一个函数将x转化为$\hat{y}$

成本函数（代价函数）

成本函数是损失函数的平均值，表示整个网络的准确性

• 例如 $J(w,b)={\sum }_{i=1}^m({\hat{y}}^{(i)}-y{)}^2/2m$ 方差公式， 来计算训练的误差（除以2更常用） 这条公式一般用于线性回归预测结果的计算
• 是关于w,b的函数，可以就成本函数找到最合适的w与b参数值
• 成本越高误差越大

回归 Regression

特定的类型的监督学习，实现对无限多可能数字的预测

• 线性回归 Linear regression 线性的回归预测模型 线性是对于基函数而言的，即基函数的线性组合 回归是指回归均值，即在低于均值时会增加靠近均值，高于均值时会减少趋近均值，可以得出一个椭圆分布的数据，其中存在均值回归线（但是具体概念需要进一步加强）

• 多元线性回归 即多个变量的线性回归 成本函数变为： $J(w,b)=\vec{w}\cdot \vec{x}+b$ 向量点乘

回归方法

• 批量（batch）梯度下降法
• 或正规方程法 一般用于后端解决参数问题

分类 Classification

输入数据，输出数据分类，只有少数的可能输出结果

• 二元分类 binary 只有两种类别

• 决策边界 当使用线性回归来拟合分类问题时，会需要一条分界线来划分0,1，这条分界线称为决策边界

分类算法

逻辑回归 logistic

• Sigmoid函数 $g(z)=1/(1+e^{-z})$ 又称逻辑函数

  Week 1-3 2024-02-28 07.49.48.excalidraw

  ⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠

  Text Elements

  1

  0.5

  -3

  3

  Link to original

  实现 逻辑回归使用线性回归函数作为Sigmoid函数的变量z $f_{w,b}(x)=g(w\cdot x+b)$ 此时函数具体值为可以为1的概率，可写为$f_{w,b}(x)=P(y=1|x;w,b)$

决策边界 对于逻辑回归，决策边界在于 z=0

损失函数 损失函数是预测的输出与真实值之间的关系，用来衡量一个预测结果的正确性 线性回归损失函数并不适用于逻辑回归(因为计算结果中局部最优值很多) 选用其他损失函数 根据最大似然估计的某种没有学过的方法，构造如下函数 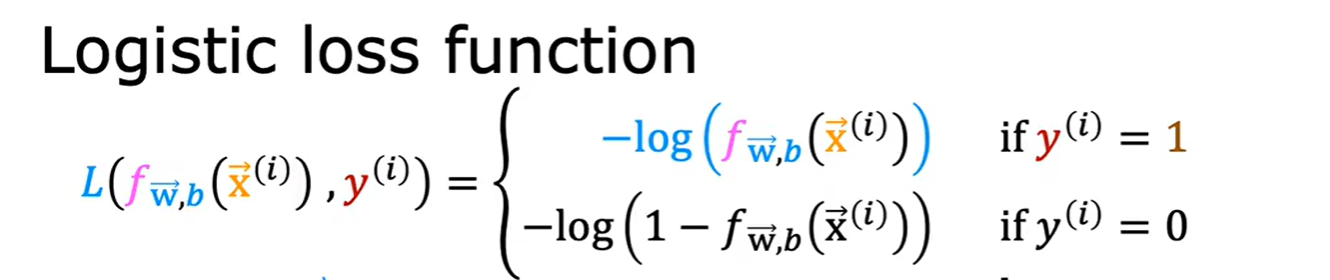- 当y实际为1，预测y越接近1则函数值越接近0 - 当y实际为0，预测y越接近0则函数值越接近0 - 化简

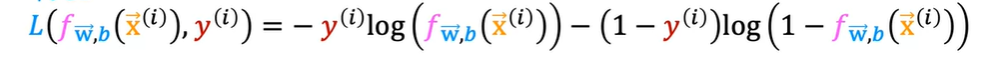
将结果计算求平均可以得到成本函数

Unsupervised learning

无监督学习

概念

没有标签属性，自己学习深入对数据的了解，从而得到结果

聚类 Clustring

猜测集群的数据类型，并将判断为同性质的聚集分为一类

• 无指定类别

异常检测 Anomaly detection

降维 Dimensionality reduction

Reinforcement learning

强化学习

梯度下降

方法

每一步找到成本函数中函数中梯度最小的方向，按照该方向最小化成本函数

• 公式 $w=w-\alpha (dJ(w,b)/dw)$ $b=b-\alpha (dJ(w,b)/db)$
  其中J函数的变量均为更新前，同步更新 当梯度变化时，每次变化的量也会变化 当导数小于0，则该方向是减少方向，即表现为加上一个数，导数大于0，即方向为增加方向，则减去一个数来反增加方向变化 其中 $\alpha$为学习率 learning rate（理解为步距，每次按这个梯度下降的方向走多远） 太小下降得慢， 太大误差大

• 局部最小 梯度下降法会带到局部最小， 线性回归只有一个最小值

• 批量梯度下降法 在梯度下降的每一步中都查看所有的训练示例

• 矢量化 矢量的运算快于逐项计算

  	for j int range(0,16)
  		f = f + w[j] * x[j]
  	
  	
  	np.dot(w,x)
  	
  	'''
  	后者在实际运算中明显快于前者，因为有针对矢量的运行机制
  	可以理解为矢量化后，数据一起被处理，因此快于逐个处理
  	'''

特征缩放

通常的，模型会在特征($x_i$)比较大的时候选择小的参数($w_i$)，在特征比较小的时候选择比较大的参数 因为微小的$x_i$变化会导致大的成本变化

• 特征缩放 将特征做变换，例如归一化（0-1）等，减少某特征对成本的影响，提高训练速度和模型能力

• 归一化 将特征缩放到(-1~1)之间 首先求出平均值 $\mu$ 由公式 $\frac{x_i-{\mu }_i}{max-min}$ 计算可得到归一化的范围

• Z-score标准化 利用正态分布标准化数据 首先求出 $\sigma$ 公式 $\frac{x_i-{\mu }_i}{{\sigma }_i}$ 计算得标准化结果

认为 当范围接近(-1~1)则没有问题，如果过于大(100)，或过于小(0.001则要做处理

梯度下降检测

• 学习曲线法 以横轴为迭代次数画成本曲线， 如果有任何一次成本变大，说明代码有错或学习率过大 -当曲线平缓时，认为训练达标
• 自动收敛测试 设置$ϵ$ ，当成本变化小于$ϵ$，则声明收敛，认为训练次数达标 但是确定合适$ϵ$很难以确定

学习率设置

当学习率过大会导致梯度下降法失效

![[Week 1 2024-02-25 08.59.43.excalidraw]]
步幅太大，会导致成本变大，同时梯度(斜率)又变大，变化累加导致成本逐渐上升

可以逐步将学习率增加三倍，找到较小的值与过大的值，尽可能选择大的学习率

特征工程 feature engineering

特征不一定是现有的，各个不同的，同样的特征与认为设计的有数学，统计意义的特征可以应用到算法中 例如面积，体积等

多项式回归

同样的特征，利用其平方，立方等构成新特征来参与算法，拟合非线性曲线

过拟合 overfit

数据拟合的结果分为三类

• 拟合不足——高偏差
• 拟合——泛化
• 过拟合——高方差

underfit ，在数据上有很大的偏差(high bias)，称为拟合不足

fit 甚至可以预测一个新的数据，有很好的泛化(generalization)

overfit 过于拟合导致预测结果失真，只适用于已有数据，精准的预测全部数据会导致拟合函数来回变化，称为高方差(high variance)

处理过拟合

• 更多训练数据

• 特征过多，但是数据较少 挑选合适的特征

正则化 regularization

参数w数值变化（b一般不变），可以保留特征，同时避免某个特征对预测的影响过大

正则化实现对所有w参数的规范化（penalize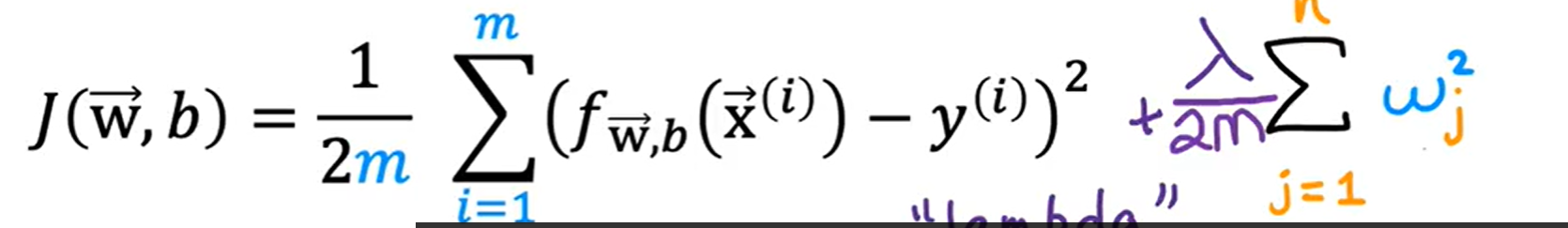） 其中，将$\lambda$ 和方差函数一起除以2m，是因为实践证明，当其除以2m之后，可以更方便的找到合适值，同时，当训练集数量变化后，$\lambda$ 值可能无需变化

这样一来，需要最小化方差函数，来拟合数据，也需要挑选$\lambda$来避免过拟合，同时成本函数维持最小化

• 如果$\lambda$太小，那么起不到正则化的作用（减低某些参数的影响）
• 如果$\lambda$太大，则影响太大，w参数会减少到很小，无法满足拟合

正则化的梯度下降法

• 对于线性回归 梯度下降法的公式几乎相同，只是成本函数变化，求导也发生变化：

  其中，b的偏导不变，因为正则化的成本函数中，b的部分没有变化 而对于w参数的更新函数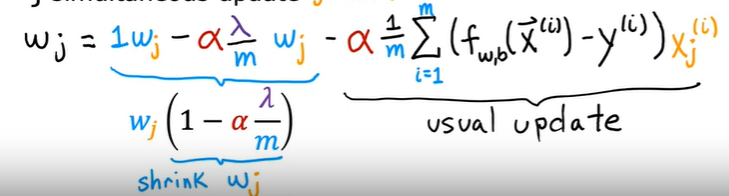$w=w-\alpha (dJ(w,b)/dw)$ 则每次更新，w都会乘上一个小于1的倍数，而且w值越大，减少就越多

• 对于逻辑回归 成本函数变化一致，即正则化公式一致，就只有逻辑回归的f(x)函数与线性回归不一样