三国游戏_(贪心，博弈)

原题链接：P1199 [NOIP2010 普及组] 三国游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意：给出n个武将，给出彼此的默契度，以默契度为战力，两人玩游戏，每次小涵先选，然后对方选择与小涵当前队列中武将默契度最高的武将，就是阻止小涵拿到与队列中武将默契度最高的武将，问是否必胜，如果胜，最后的默契度是多少

思路

是经典的博弈，对方每次贪心的选，是否存在策略使得必胜，每个武将的最佳搭配肯定选不了，那如果要赢，最好就是选择次大中的最大

首先，次大的最大肯定选得到，只要首次就选择次大所在的行的武将就可以在对方挑走最大后，选走次大

但是这样是否一定能赢呢？

要分情况看：

• 对方选择的武将是与我们之前选的武将相交（即阻止的是之前武将的匹配） 之前武将的最大值已经被阻止，次大的最大已经被选了，此时与其之前的武将有相交，即确定了一个组合
  • 此值为最大 反证：如果为最大，比三角形还大，三角形又比五角星大，那三角形就是最大的次大，不符合假设
  • 此值大于五角星 反证：如果此值大于五角星，小于三角形，那么此值就是最大的次大，不合题意

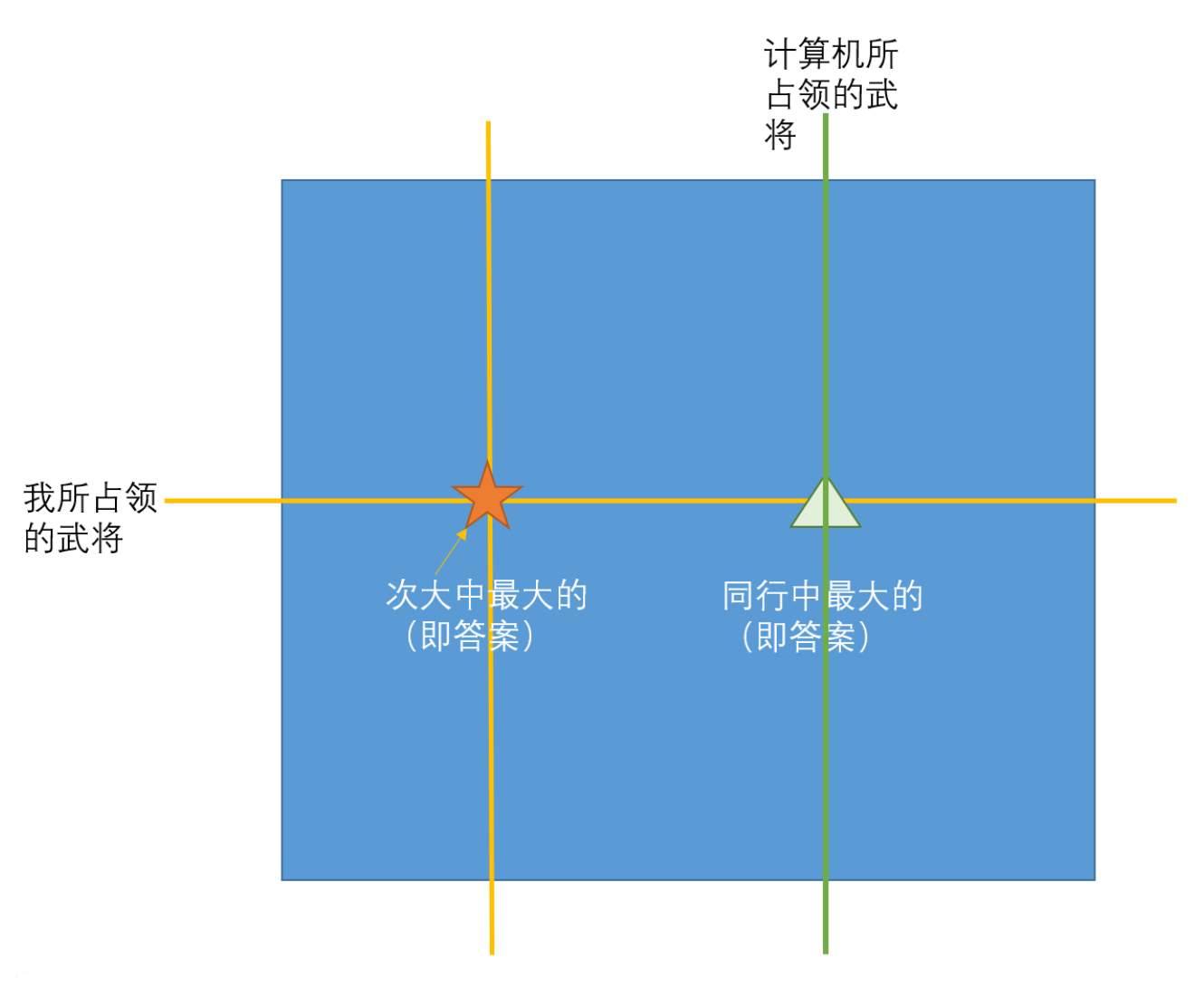
也就是说不可能比所选的次大中的最大还大

也就是必胜

代码

#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 550;
int a[N][N];
int n;
 
int main()
{
    cin >> n;
 
    int ans = 0;
    for(int i = 0; i < n; i ++)
    {
        int res_m = 0;
        for(int j = i + 1; j < n; j ++)
        {
            cin >> a[i][j];
            a[j][i] = a[i][j];
        }
 
        sort(a[i], a[i] + n);
        res_m = a[i][n - 2];
        //cout << res_M << endl << res_m << endl;
        ans = max(ans, res_m);
        //cout << res_m << endl;
    }
 
    cout << "1" << endl;
    cout << ans << endl;
 
    return 0;
}