原题链接:P5441 【XR-2】伤痕 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题意:多座城市修建道路,其中双向道路数量有限,单向无限,每每两座城市都要有道路,问怎么建,选择4座可以互相到达(不用经过除这4座城市外的其他城市)的方案数最多
思路
所谓构造就是看缘分或数学
分类讨论很重要
首先分类讨论,什么样的城市(4个点)不能被选为目标城市,然后看看能不能尽量减少这些情况(称为非强连通)
- 一座城市向其他三座城市单向
- 三座城市向一座城市单向
- 有城市间双向,但是以双向的城市为一小组,其组间都是一个方向的单向
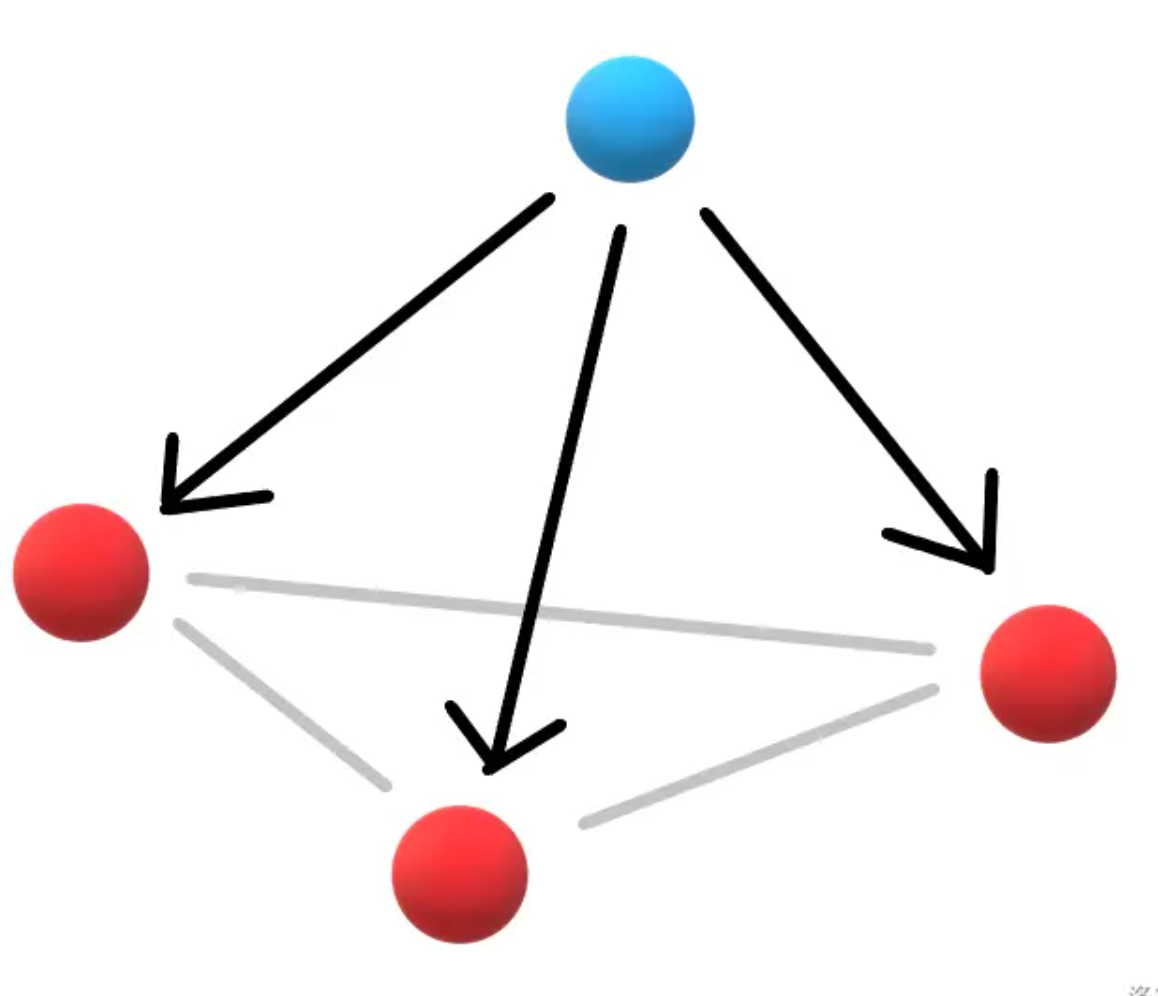
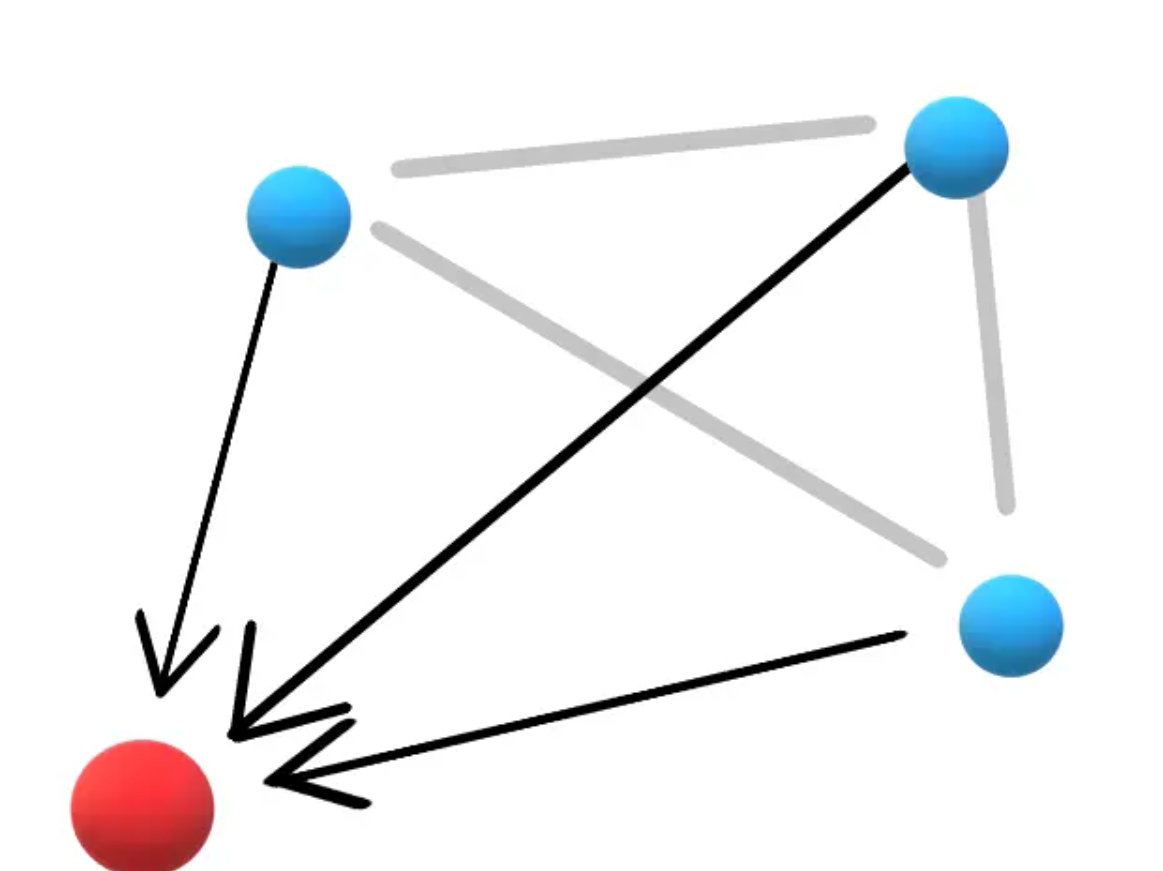
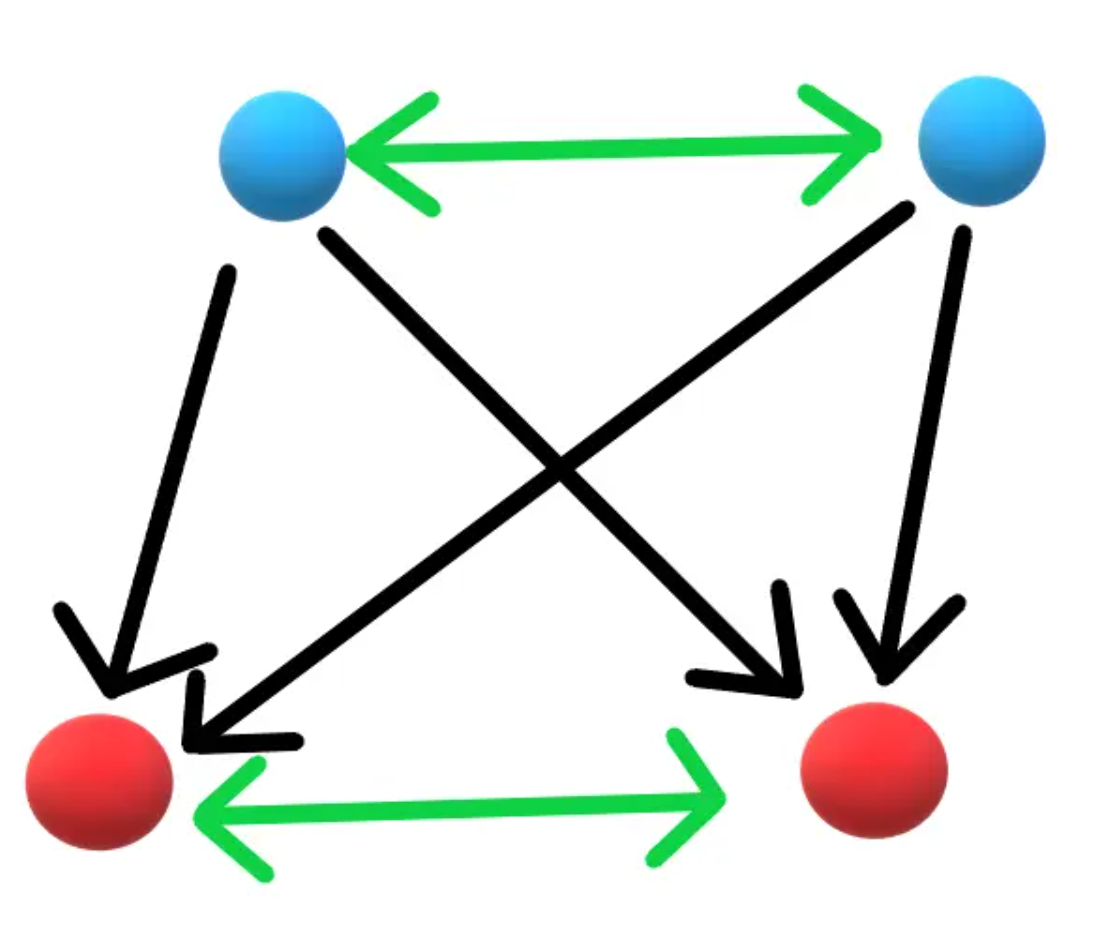 这三组中,如果不是第一类,才可能是第二类
这三组中,如果不是第一类,才可能是第二类
观察各类
第一类
如果一个城市有S单向道,那么其有种可能为第一类,而单向道的总数为总道路数减去双向道路数 ,有
设
求导
发现,当x>2时,f(x)为凹函数,此时满足p+q为常数,p和q差值越小,f(p)+f(q)越小
即让x越接近,结果越小,也就是将间差距最小,直接令其相等,可以得到第一类最小的数量
第二类第三类
最少可以没有
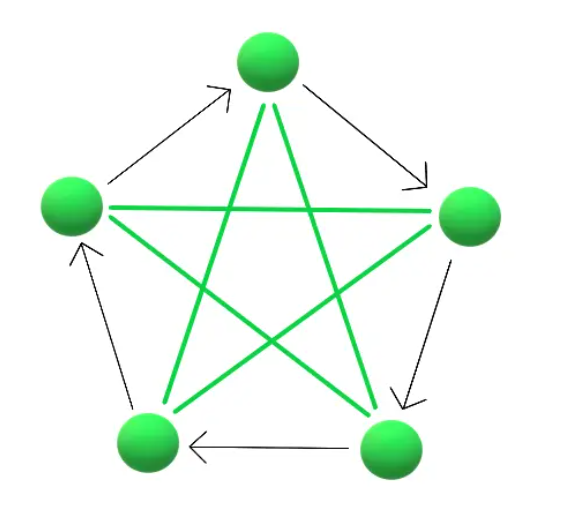
构造形式如上,每点顺时针单向连接,每点同时与最远的点双向连接(刚好为n)
即满足第二和第一为第一 第三不满足
即最终答案为:
代码
#include <bits/stdc++.h>
//题解
using namespace std;
const int N = 110;
int g[N][N];
int n;
int main()
{
cin >> n;
if(n == 1)
{
cout << '0' << endl << '0' << endl;
return 0;
}
for(int i = 0; i < n; i ++)
{
for(int j = i + 1; j <= i + (n + 1) / 2; j ++)
{
g[i][j % n] = 1;
}
}
int ans = n * (n - 3) * (n * n + 6 * n - 31);
cout << ans / 48 << endl;
for(int i = 0; i < n; i ++)
{
for(int j = 0; j < n; j ++)
cout << g[i][j] << ' ';
cout << endl;
}
return 0;
}