聚类

什么是聚类

在 “无监督学习”(unsupervised learning)中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础

聚类则是试图将数据集的样本划分为若干个互不相交的类簇，从而每个簇对应一个潜在的类别。

聚类直观来说就是将相似的样本聚在一起，形成一个类簇(cluster)，因此如何度量相似性(similarity measure)将作为首要问题，这又称为距离度量，而性能度量为评价聚类的好坏提供了一系列有效性指标

距离度量

几类常用的度量方法

一般的，距离度量方法要满足一些基本性质：

• 非负性：$dist(x_i,x_j)\ge 0$
• 同一性：$dist(x_i,x_j)=0当且仅当x_i=x_j$
• 对称性：$dist(x_i,x_j)=dist(x_j,x_i)$
• 直递性：$dist(x_i,x_j)\le dist(x_i,x_k)+dist(x_k,x_j)$

其中，直递性同时也是三角不等式，两边之和大于第三边

常用的距离度量方法是：闵可夫斯基距离(Minkowski distance)

$${\text{dist}}_{\text{mk}}({\mathbf{x}}_i,{\mathbf{x}}_j)={\left(\sum _{u=1}^n|x_{iu}-x_{ju}{|}^p\right)}^{\frac{1}{p}}$$

当p=1时，闵可夫斯基即曼哈顿距离(Manhattan distance)

$${\text{dist}}_{\text{man}}({\mathbf{x}}_i,{\mathbf{x}}_j)=||{\mathbf{x}}_i-{\mathbf{x}}_j|{|}_1=\sum _{u=1}^n|x_{iu}-x_{ju}|$$

当p=2时，即欧式距离(Euclidean distance)

$${\text{dist}}_{\text{ed}}({\mathbf{x}}_i,{\mathbf{x}}_j)=||{\mathbf{x}}_i-{\mathbf{x}}_j|{|}_2=\sqrt{\sum _{u=1}^n|x_{iu}-x_{ju}{|}^2}$$

属性分为连续属性和离散属性，对于训练值的属性，一般可以被学习器所用，有时会根据具体的情形做相应的预处理：例如归一化等，离散值则需要进一步处理：

• 如果属性之间存在序关系，则将其转化为连续值，例如 高、中等、矮可转换为 {1, 0.5, 0}
• 如果不存在序关系，则转化为向量形式，例如：性别可转换为{(1, 0), (0, 1)}

连续属性和离散属性都可以直接参与计算，其反映一种程度关系，称为有序属性，而对于不存在序关系的离散属性，称为无需属性

对于无需属性，一般采用VDM进行距离的计算，其定义为：

$${\text{VDM}}_p(a,b)=\sum _{i=1}^k{\left|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right|}^p$$

其中：

• $u$ 是某个离散属性
• $k$ 是类别总数
• $m_{u,a}$ 是属性$u$取值为$a$的样本总数
• $m_{u,a,i}$ 属性$u$取值为$a$且真实类别为$i$的样本数

$\frac{m_{u,a,i}}{m_{u,a}}$ 就是经验概率 $P(类=i|u=a)$

所以VDM可以写为：

$${\text{VDM}}_p(a,b)=\sum _{i=1}^k|P(i\mid u=a)-P(i\mid u=b){|}^p$$

通过经验概率将离散属性改为连续属性，度量 a，b在所有类别分布上的距离

于是，计算两个样本之间的距离时，可以将闵可夫斯基距离和VDM混合一起计算

$${\text{MinkovDM}}_p({\mathbf{x}}_i,{\mathbf{x}}_j)={\left(\underset{\text{有序属性}}{\underbrace{\sum _{u=1}^{n_c}|x_{iu}-x_{ju}{|}^p}}+\underset{\text{无序属性}}{\underbrace{\sum _{u=n_c+1}^n{\text{VDM}}_p(x_{iu},x_{ju})}}\right)}^{\frac{1}{p}}$$

对于聚类而言，这些距离的度量方法可以被用于度量相似性，此时就不一定满足上述四个基本性质，这种方法也称为非度量距离(non-metric distance)

性能度量

聚类算法有两种聚类性能度量指标：外部指标和内部指标

外部指标

将聚类结果与某个参考模型的结果进行比较，以参考模型的输出作为标准，评价聚类的好坏

定义

$$\begin{array}{rl}a& =|SS|,SS=\{(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j\}\\ b& =|SD|,SD=\{(x_i,x_j)|{\lambda }_i={\lambda }_j,{\lambda }_i^{\ast }\ne {\lambda }_j^{\ast },i<j\}\\ c& =|DS|,DS=\{(x_i,x_j)|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{\ast }={\lambda }_j^{\ast },i<j\}\\ d& =|DD|,DD=\{(x_i,x_j)|{\lambda }_i\ne {\lambda }_j,{\lambda }_i^{\ast }\ne {\lambda }_j^{\ast },i<j\}\end{array}$$

其中：

• $\lambda$ 代表聚类结果，${\lambda }^{\ast }$ 代表参考结果
• $a$ 代表聚类结果属于同一类，参考结果也属于同一类
• $b$ 代表聚类同类，参考不同
• $c$ 代表聚类不同，参考相同
• $d$ 代表聚类不同，参考不同

基于这四个值可以计算出一些常用的外部评价指标

• Jaccard系数(Jaccard Coefficient)，简称JC

$$\text{JC}=\frac{a}{a+b+c}$$

• FM指数(Fowlkes and Mallows Index)，简称FMI

$$\text{FMI}=\sqrt{\frac{a}{a+b}\cdot \frac{a}{a+c}}$$

• Rand指数(Rand Index)，简称RI

$$\text{RI}=\frac{2(a+d)}{m(m-1)}$$

m是样本数

其范围均是$(0,1)$ ，取值越大越好

内部指标

簇内高内聚，簇间低耦合

$$\begin{array}{rl}\text{avg}(C)& =\frac{2}{|C|(|C|-1)}\sum _{1\le i<j\le |C|}\text{dist}(x_i,x_j)\\ \text{diam}(C)& =\underset{1\le i<j\le |C|}{\max }\text{dist}(x_i,x_j)\\ d_{\min }(C_i,C_j)& =\underset{x_i\in C_i,x_j\in C_j}{\min }\text{dist}(x_i,x_j)\\ d_{\text{cen}}(C_i,C_j)& =\text{dist}({\mu }_i,{\mu }_j)\end{array}$$

分别是：

• 簇内平均距离（越小越好）
• 簇内最大距离（越小越好）
• 簇间最小距离（越大越好）
• 簇中心距离（越大越好）

基于上述四个距离，可以得到一下常用的内部指标

• DB指数(Davies-Bouldin Index)，简称DBI，越小越好

$$\begin{array}{rl}\text{DBI}& =\frac{1}{k}\sum _{i=1}^k\underset{j\ne i}{\max }\left(\frac{\text{avg}(C_i)+\text{avg}(C_j)}{d_{\text{cen}}({\mu }_i,{\mu }_j)}\right)\end{array}$$

• Dunn指数(Dunn Index)，简称DI，越大越好

$$\begin{array}{rl}\text{DI}& =\underset{1\le i\le k}{\min }\left\{\underset{j\ne i}{\min }\left(\frac{d_{\min }(C_i,C_j)}{{\max }_{1\le l\le k}\text{diam}(C_l)}\right)\right\}\end{array}$$

另外几类外部评价指标

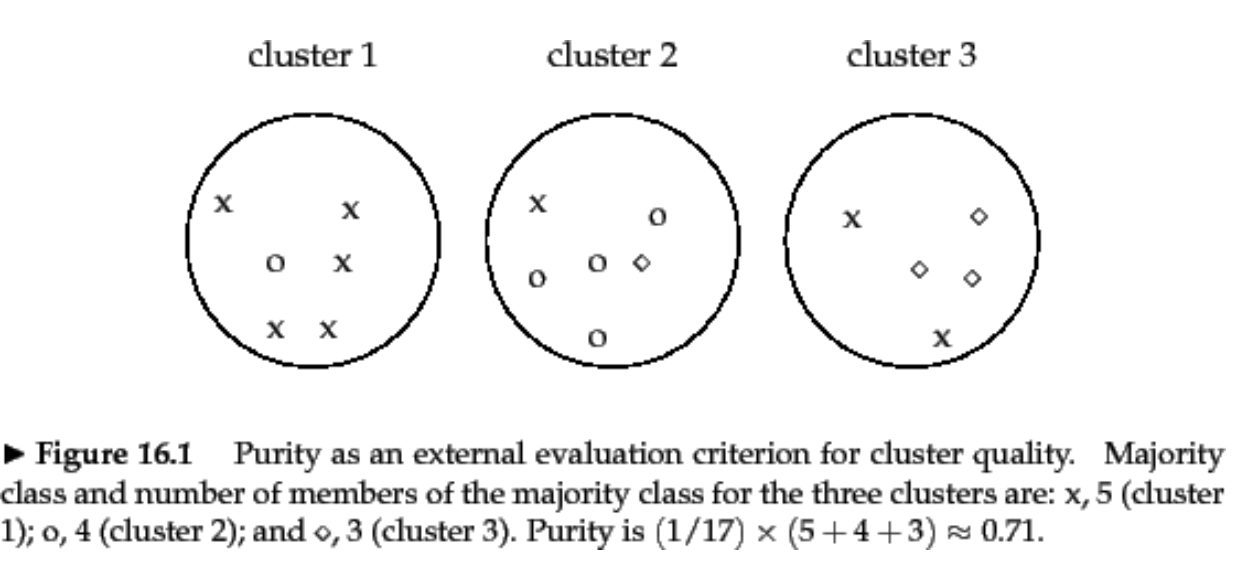
纯净度(Purity)

$$\begin{array}{rl}\text{Purity}(\Omega ,C)& =\frac{1}{N}\sum _k\underset{j}{\max }|w_k\cap c_j|\end{array}$$

其中，$N$表示总的样本个数，$\Omega$表示聚类簇的划分，$C$表示真实类别的划分

• 给每个聚类簇分配一个类别，这个类别的样本在该簇中出现的次数最多，然后计算K个聚类簇的这个次数之和，再进行除以$N$ 归一化
• 无法用于权衡聚类质量与簇个数之间的关系

NMI(Normalized Mutual Information)

归一化互信息

$$\begin{array}{rl}\text{NMI}(\Omega ,C)& =\frac{I(\Omega ;C)}{(H(\Omega )+H(C))/2}\end{array}$$

其中，$I$ 表示互信息，H为熵，当 $log$ 取 2 为底时，单位为 bit，取e为底时单位为nat（熵值定义见 信息熵）

$$\begin{array}{rl}I(\Omega ;C)& =\sum _k\sum _{j}P(w_k\cap c_j)\log \frac{P(w_k\cap c_j)}{P(w_k)P(c_j)}\\ & =\sum _k\sum _j\frac{|w_k\cap c_j|}{N}\log \frac{N|w_k\cap c_j|}{|w_k||c_j|}\end{array}$$

其中，$P(w_k)$，$P(c_j)$ ,$P(w_k\cap c_j)$ 可以分别看作样本属于聚类簇$w_k$，属于类别$c_j$ ，同时属于两者的概率，并依据概率的极大似然估计推导，得到第二个式子

$$\begin{array}{rl}H(\Omega )& =-\sum _{k}P(w_k)\log P(w_k)\\ & =-\sum _k\frac{|w_k|}{N}\log \frac{|w_k|}{N}\end{array}$$

互信息表示给定类簇信息$C$ ，类别信息$\Omega$ 的增加量，或者说不确定度的减少量

可以直观的写为：

$$\begin{array}{rl}I(\Omega ;C)& =H(\Omega )-H(\Omega |C)\end{array}$$

• 互信息的最小值为0，当类簇相对于类别是独立随机的，$\Omega$ 对 $C$ 没有带来任何有用信息
• $\Omega$ 与 $C$ 关系越密切，那么 $I(\Omega ;C)$ 越大，如果 $\Omega$ 完整重现了$C$ ，则互信息最大（熵值$H(\Omega |C)$为0）
• 当 $K=N$ 时,即类簇数和样本个数相等，MI 也能达到最大值。所以 MI 也存在和纯度类似的问题,即它并不对簇数目较大的聚类结果进行惩罚，因此也不能在其他条件一样的情况下，对簇数目越小越好的这种期望进行形式化

而NMI则可以解决上述问题，因为熵会随簇的数目增大而增大，当$K=N$ 时，$H(\Omega )$ 会达到最大值 $logN$ ，使得 $NMI$ 保持比较低

Note

为什么采用$H(\Omega )+H(C))/2$

因为它是 $I(\Omega ,C)$ 的 紧上界，保证NMI 归一化

计算步骤

1. 计算联合概率分布
2. 计算边际分布
3. 计算熵和互信息
4. 归一化计算NMI

详见：[ML] 聚类评价指标 - 知乎

ACC

用于比较获得标签与数据提供的真实标签

$$\begin{array}{rl}AC& =\frac{{\sum }_{i=1}^n\delta (s_i,\text{map}(r_i))}{n}\end{array}$$

其中，$r,s$ 表示数据$x_i$ 对应的标签和真实标签，n为样本数，$\delta$ 表示指示函数

$$\begin{array}{r}\delta (x,y)=\{\begin{array}{ll}1& \text{if }x=y\\ 0& \text{otherwise}\end{array}\end{array}$$

map时最佳类标的重现分配，保证统计的正确，一般最佳重分配通过匈牙利算法（Kuhn-Munkres or Hngarian Algorithm）实现，在多项式时间里求解分配问题

Note

为什么重分配？

因为得到的聚类结果和真实标签的 数值 可能不一一对应，可能同一簇但标签不同，需要重映射来做对比

原型聚类

基于原型的聚类

通过参考一个模板向量或模板分布的方式来完成聚类，例如K-Means基于簇中心来实现聚类，混合高斯聚类则基于簇分布来实现聚类

K-Means

先随机指定类中心，根据样本与类中心的远近划分类簇，再重新计算类中心（属于一个簇的算一个中心点），迭代直到收敛。迭代过程并非主观想象，事实上若将样本的类别看作“隐变量”（latent variable)，类中心看作样本的分布参数，这个过程实际上就是EM算法的两步走策略，其根本的目的就是为了最小化平方误差函数E

$$E=\sum _{i=1}^k\sum _{\mathbf{x}\in C_i}||\mathbf{x}-{\mathbf{\mu }}_i|{|}_2^2$$

学习向量量化(IVQ)

LVQ也是基于原型的聚类算法，使用样本的真实类标记辅助聚类，首先LVQ根据样本的类标记，从各类中随机选出一个样本作为该类的原型，组成一个原型特征向量组，再从样本集中随机挑选一个样本，计算其与原型向量组中每个向量的距离，选取距离最小的原型向量所在的类簇作为划分结果，再与真实类标比较

• 如果划分结果正确，则让原型向量离这个样本近一些
• 如果划分不正确，让原型向量离这个样本远一些

高斯混合聚类

高斯混合聚类采用高斯分布来描述原型，假设每个类簇中的样本都服从一个多维高斯分布，那么空间中样本可以看作由k个多维高斯分布混合而成的

对于多维高斯分布，其概率密度函数如下：

$$p(\mathbf{x})=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\mathbf{\Sigma }{|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(\mathbf{x}-\mu {)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mu )}$$

其中，$\mu$ 表示均值向量，$\Sigma$ 表示协方差矩阵，看出一个多维高斯分布完全由这两个参数决定，定义高斯混合分布为：

$$p_{\mathcal{M}}(\mathbf{x})=\sum _{i=1}^k{\alpha }_i\cdot p(\mathbf{x}\mid {\mu }_i,{\mathbf{\Sigma }}_i)$$

称$\alpha$ 为混合系数，这样空间中样本的采样过程可以抽象为：

1. 选择一个簇（高斯分布）
2. 根据对应的高斯分布密度函数进行采样

此时采用贝叶斯公式：

$$\begin{gathered} p_{\mathcal{M}}(z_j=i\mid {\mathbf{x}}_j)=\frac{P(z_j=i)\cdot p_{\mathcal{M}}({\mathbf{x}}_j\mid z_j=i)}{p_{\mathcal{M}}({\mathbf{x}}_j)} \\ =\frac{{\alpha }_i\cdot p({\mathbf{x}}_j\mid {\mu }_i,{\mathbf{\Sigma }}_i)}{{\sum }_{l=1}^k{\alpha }_l\cdot p({\mathbf{x}}_j\mid {\mu }_l,{\mathbf{\Sigma }}_l)} \end{gathered}$$

此时只需要选择 $p_{\mathcal{M}}$ 最大时的类簇并将该样本划分到其中。

Note

这一步是贝叶斯吗？

实际上不是，这一步开始就是EM算法，朴素贝叶斯无法解决这个问题是因为似然函数中存在一个隐变量$z_i$，其含义是当前数据点属于哪个分布，这在式子中没有显示指明（只是要求归属那一类时最大），所以此时使用EM算法，先引入$z_i$ ，计算E步（上述公式），再计算M步（最大化）

从贝叶斯分类角度来看，这里其实 $P(z_j=i)$ 就是类先验，$p_{\mathcal{M}}({\mathbf{x}}_j\mid z_j=i)$ 就是类条件。但这里没有真实类标信息，对于类条件概率，并不能像贝叶斯分类那样通过最大似然法美好地计算出来(见贝叶斯分类器），因为这里的样本可能属于所有的类簇，这里的似然函数变为：

$$LL(D)=\ln \left(\prod _{j=1}^m{p}_{\mathcal{M}}({\mathbf{x}}_j)\right)=\sum _{j=1}^m\ln \left(\sum _{i=1}^k{\alpha }_i\cdot p({\mathbf{x}}_j|{\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i)\right)$$

其中 $j$ 是遍历样本，$i$ 是遍历类簇

最大似然法计算不出所有的参数，应该用EM算法，对高斯分布的参数进行随机初始化，计算各个$p_{\mathcal{M}}$ ，再最大化似然函数(对$LL(D)$分别求参数的偏导)，迭代更新

$${\mathbf{\mu }}_i=\frac{{\sum }_{j=1}^m{\gamma }_{ji}{\mathbf{x}}_j}{{\sum }_{j=1}^m{\gamma }_{ji}}$$ $${\mathbf{\Sigma }}_i=\frac{{\sum }_{j=1}^m{\gamma }_{ji}({\mathbf{x}}_j-{\mathbf{\mu }}_i)({\mathbf{x}}_j-{\mathbf{\mu }}_i{)}^T}{{\sum }_{j=1}^m{\gamma }_{ji}}$$ $${\alpha }_i=\frac{1}{m}\sum _{j=1}^m{\gamma }_{ji}$$

密度聚类

密度聚类从样本角度考察样本之间的可连接行，基于可连接性拓展疆域（类簇），最著名的算法时 DBSCAN 算法

• $ϵ$-邻域: 对 $x_j\in D$，其 $ϵ$-邻域包含样本集 $D$ 中与 $x_j$ 的距离不大于 $ϵ$ 的样本，即 $N_{ϵ}(x_j)=\{x_i\in D\mid \text{dist}(x_i,x_j)\le ϵ\}$；
• 核心对象 (core object): 若 $x_j$ 的 $ϵ$-邻域至少包含 $MinPts$ 个样本，即 $|N_{ϵ}(x_j)|\ge MinPts$，则 $x_j$ 是一个核心对象；
• 密度直达 (directly density-reachable): 若 $x_j$ 位于 $x_i$ 的 $ϵ$-邻域中，且 $x_i$ 是核心对象，则称 $x_j$ 由 $x_i$ 密度直达；
  • (必须在邻域中)
• 密度可达 (density-reachable): 对 $x_i$ 与 $x_j$，若存在样本序列 $p_1,p_2,\dots ,p_n$，其中 $p_1=x_i,p_n=x_j$ 且 $p_{i+1}$ 由 $p_i$ 密度直达，则称 $x_j$ 由 $x_i$ 密度可达；
  • (即为传递性，并不一定要在邻域内)
• 密度相连 (density-connected): 对 $x_i$ 与 $x_j$，若存在 $x_k$ 使得 $x_i$ 与 $x_j$ 均由 $x_k$ 密度可达，则称 $x_i$ 与 $x_j$ 密度相连。

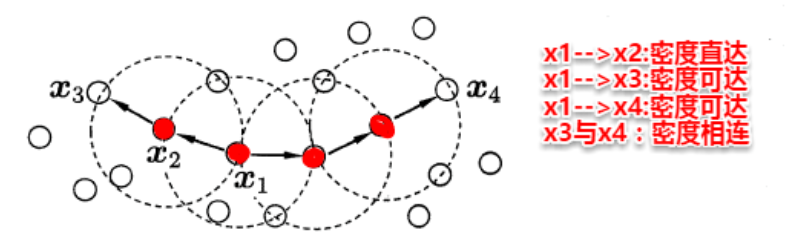
DBSCAN是找出一个核心对象所有密度可达的样本集合形成簇，找到一个核心对象A，找到所有密度可达的样本集合，形成一个密度相连的类簇，直到所有的核心对象都遍历完。

层次聚类

树形结构的聚类方法，自底向上结合策略(AGNES算法），其基本步骤是：

1. 初始化，将每个样本归为一类，计算两类之间的距离，也就是样本之间的相似度
2. 寻找相似度最大的两个类，归为一类
3. 重新计算新产生成的这个类与各个旧类之间的相似度
4. 重复2，3直到样本都归于一类

衡量相似度有多个方法：

• 单链接(single-linkage)，取类间最小距离

$$\text{最小距离: }{d}_{\min }(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\min }\text{dist}(x,z)$$

• 全链接(compelte-linkage)，取类间最大

$$\text{最大距离: }{d}_{\max }(C_i,C_j)=\underset{x\in C_i,z\in C_j}{\max }\text{dist}(x,z)$$

• 均链接(average-linkage)，取类间两两平均距离

$$\text{平均距离: }{d}_{\text{avg}}(C_i,C_j)=\frac{1}{|C_i||C_j|}\sum _{x\in C_i}\sum _{z\in C_j}\text{dist}(x,z)$$

Refer

• 西瓜书
• 西瓜书学习笔记(10)—聚类 - Heywhale.com
• [ML] 聚类评价指标 - 知乎