二分图

基本概念

- 对于二分图问题，时间复杂度不用过多考虑，一般虽然时间复杂度高，但是运行结果很好
- #### 二分图
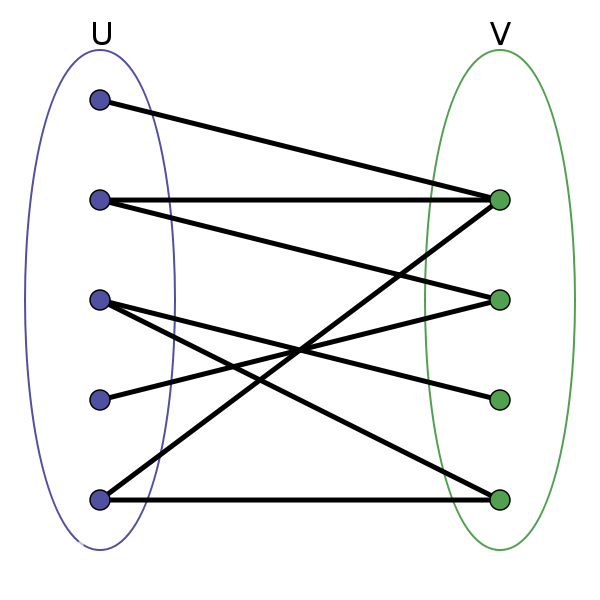
	- 就是一分为二的图
	- 两边各是点的集合，中间是点与点的连线

{:height 2, :width 2} - 理论上，二分图不含奇数环 - 当存在奇数环，在染色过程中，会发现起点位置（环起点）会被染成两种颜色，即有一个点于二分图的定义存在矛盾（同时在两边），所以不行。 - 匹配 - 任意两条边不依附于同一顶点 - 就是说，多于一条边，且这些边不存在相同的顶点，此时这些边及顶点构成的子图称为匹配 - 最大匹配 就是匹配的最大可能

• 具体实现

  • 染色法

    collapsed:: true

    • 概念

      • 染色法用来判断是否为二分图
      • 用不同颜色标志不同集合，每次对一个点染色，例如黑色，如果是二分图，则该点所有邻接点都是另一颜色（例如白色），如果染色中出现邻接点颜色相同，则说明该图不是二分图

    • 实现

      • 通过图的查找
        • DFS或BFS
        • 查找未染色的结点染色，如果染过色了就对比与当前邻接点是否颜色相同
      • 用 1， 2代表两种颜色

    • 代码

      • AC_color.cpp

			  以下是DFS实现
			  要注意的是递归处理，递归可以形象性的理解，当调用函数了，就相当于说做了某中处理
			  抽象是抽象，但是要意会
			  
			  
			  //实现为发生错误时返回false
			  bool dfs(int u, int c)
			  {
			    	color[u] = c;
			    	for(int i = h[u]; i != -1; i = ne[i])
			      {
			        	int j = e[i];
			        	if(!color[j])  //还没染色
			          {
			            	if(!dfs(j, 3 - c)) // 染色，在染色时发生错误
			                return false;
			          }
			        	else
			        		if(color[j] == c)  // 判断出错，如果染色了，但是颜色与当前邻接点相同
			                	return false;
			  	}
			    
			    return true;
			  }

- ### 匈牙利算法
	- **查找最大匹配**
	- #### 实现
		- 先建立好邻接表
		- 只查找表的一边（首先得是二分图）
			- 在查找时，判断当前点是否有与另一边的连线，有就先标记，当查找到有两个点对应的另一边顶点为同一个时，对先查找到的点再查看是否有其他对应点，有就更改先前点的对应点，再继续查找。没有就找当前点的其他对应点，再依次判断
		- 找完一边的所有点后，算法结束，此时记录的匹配数就是最大匹配
	- #### 代码
		- [AC_Hungary.cpp](../assets/AC_Hungary_1700281272858_0.cpp)
		- ```C++
		  int match[N];  // 不会更新，记录另一边点对应的点
		  bool st[N];  //st是每次查找都会更新的，标志另一边的点在这次查找是否已经找过
		  
		  
		  bool find(int u)
		  {
		    	for(int i = h[u]; i != -1; i = ne[i])
		      {
		        	int j = e[i];
		        	if(!st[i])
		          {
		            	st[j] = true;  // 找过
		            	if(match[j] == 0 || find(match[j])) // 如果该点还没匹配或者匹配的点可以再找
		           		return true;
		          }
		      }
		    
		    	return false;
		  }
		  
		  
		  for(int i = 1; i <= n; i ++)
		  {
		    	memset(st, false, sizeof st);
		    	if(find(i))  ans ++;
		  }
		  ```
	-